シグモイド関数を分類に使う理由は確率を表すから

二値分類（男か女かなど2つのラベルのどちらかを予測する問題）を扱うと活性化関数にシグモイド関数というものをよく見かけると思います。

機械学習を学んでいるとシグモイド関数は活性化関数として当たり前のように導入されて確率を表現すると書かれていたりしますよね。

そもそも活性化関数とは何のためにあるのでしょうか？またなぜシグモイド関数は分類問題の活性化関数として使われるのでしょうか？基本に立ち返って考えていきましょう。

活性化関数は出力の意味づけを行う

活性化関数はパーセプトロンやニューラルネットワークなどのアルゴリズムに登場し、入力に対して何かしらの演算を行なって出力を返す役割を持っています。

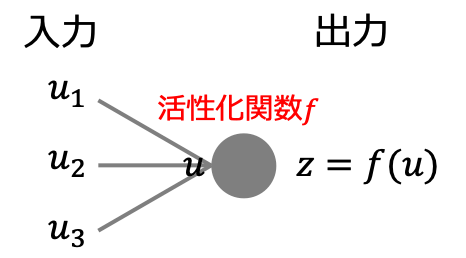
活性化関数は受け取った入力に対して返す出力に意味を持たせる役割を果たしていて、持たせる意味に応じて様々な種類の関数があります。

では分類問題におけるシグモイド関数はどのような意味を持つかというと、出力のラベルが1（または0）である確率を表しています。なぜシグモイド関数は確率を表していると言えるのか説明していきます。

シグモイド関数は確率を意味づける

シグモイド関数（別名ロジスティック関数）とは下のように表される関数を指し、入力に対して出力が(0,1)となる関数です。

$$f(u) = \frac{1}{1+e^{-u}}$$

グラフに表すと下図のような形状となり、確かに入力に対してラベルが1（または0）である確率を表現する関数としては適していそうです。

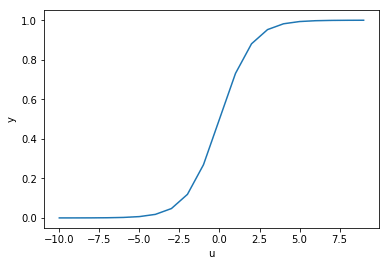
しかしなぜ活性化関数にシグモイド関数が使われているのでしょうか。別に入力に対して出力が(0,1)であるそれらしい関数であれば何でもいい気がします。

結論から言えば活性化関数に使う関数はなんでも良いのです。確率はあくまで私たちの解釈であって絶対的な正解などありません。ですがシグモイド関数が確率を意味づける関数としてよく使われているのは主に次のような理由です。

• 関数の導入背景がわかりやすい
• 計算が単純
• 二値分類に限らず多クラスの分類にも拡張が可能

以上の項目について紹介していきます。

関数の導入背景がわかりやすい

まずはシグモイド関数がどのように導入されたのか背景を紹介します。

ある事象の起こりやすさを表す指標としてオッズ比というものがあります。オッズ比とは事象が起こる確率と起こらない確率の比$\frac{p}{1-p}$で表されます。

ここでオッズ比の対数をとったロジット関数というものを考えます。

$$logit(p) = \log\frac{p}{1-p}$$

ロジット関数を導入すると(0,1)の入力値を実数全体の値に変換することができます。ロジット関数は事象の起こりやすさを実数全体の値に変換できるため、「事象の起こりやすさ」と「データの特徴量」を結びつけることが可能となりました。

$$logit(p(y=1|\bm{x}) = w_0x_0+w_1x_1+\cdots+w_nx_n$$

さてここからなにが言えるでしょう？

ロジット関数の逆関数を考えれば特徴量を入力として事象の起こりやすさを求めることができるということです。ロジット関数の逆関数こそがシグモイド関数（ロジスティック関数）なのです。

このような背景からシグモイド関数は特徴量を入力としてラベルの確率を表す用途に用いられているのです。

計算が単純

シグモイド関数が使われる理由として微分計算が簡単という一面もあります。

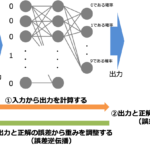
ニューラルネットワークの逆伝播計算では活性化関数の微分計算を必要としますが、シグモイド関数の微分は下のようにシグモイド関数自身を用いて表すことができます。

$$\begin{aligned} f’(u) &= \frac{1}{(1+e^{-u})^2} \dot -e^{-u} \\ &= \frac{1}{1+e^{-u}} \dot (1-\frac{1}{(1+e^{-u})^2}) \\ &= f(u)(1-f(u))\end{aligned}$$

何回微分しても元の関数で表すことができるため複雑な微分計算を避けることができるのです。

多クラスの分類にも拡張が可能

二値分類においてシグモイド関数はラベルが1であるかそうでないか（ラベルが0である）の確率を表現していました。

この考え方は他クラス分類においても同じことが言えます。ラベルがK個あるときに出力がラベルiであるかそうでないか（ラベルi以外のK-1個のラベル）の確率を表すことができれば二値分類を自然に他クラス分類に拡張することができます。

他クラス分類への拡張を可能としている活性化関数がsoftmax関数と呼ばれるものです。softmax関数の出力を$y_k$とおくと下のような表式となります。

$$y_k = \frac{\exp{(u_k)}}{\sum^K_j\exp{(u_j)}}$$

二値分類を考えると$K=2$であるので下のように変形するとシグモイド関数となることが確認できます。

$$\begin{aligned} y_1 &= \frac{\exp(u_1)}{\exp(u_0)+\exp(u_1)} \\ &= \frac{1}{1+e^{(u_0-u_1)}}\end{aligned}$$

またsoftmax関数の出力の和$\sum_k y_k=1$であることからもsoftmax関数の出力がラベルkである確率を表現していると考えられます。

以上の観点からシグモイド関数は分類問題に使われる代表的な活性化関数として使われてきたのです。

まとめ