量子コンピュータを学ぶ上で根底にある量子力学という物理を知ることはとても大切です。
量子力学とは量子という非常に小さなモノの振る舞いを記述する物理のことで非常に難解な学問として有名です。物理を専門にする人達でも理解することは容易ではありません。
なぜならこの「量子」というものは私たちの常識では考えられないような性質を持って不思議な振る舞いをするからです。
この記事では量子の持つ不思議な性質がなぜ量子コンピュータに活かされているのかについて紹介します。
量子は粒子であり波である
量子の最も不思議な性質は粒子と波の性質を両方持つことです。意味がわかりませんよね。
まず量子が粒子の性質を持っているというのは直感に反しないと思います。粒子の性質とは、物体を1つ、2つと数えることができて同じ場所に複数の物体が共存できないというものです。
中学高校で物質は原子によって構成されているとを習いましたよね。量子とは原子そのものや原子を構成する物質の総称です。そのため量子が粒子のように振舞うというのは当たり前のように思えます。
では波の性質とは何か?
波と聞いてまず思いつくのは下のような水が波打っている様子ですよね。物理では音波や電磁波も同様に波として扱います。これらの「波」に共通する性質は2つあります。
- 空間的に広がっていて1つ、2つと数えられない
- 同じ場所に複数の波が共存して影響を及ぼし合う(重ね合わせ)
何か違和感を感じませんか?先ほどと言っていることが真逆です。そうです、これが量子が持つ最も不思議な性質です。量子はある時は粒子として、ある時は波として振舞うことが知られています。
この不思議な性質を検証した実験に二重スリット実験というものがあります。下の動画から量子の不思議な性質を感じ取ってもらえると思います。
量子の性質を計算に用いる
ではこの量子の不思議な性質をどのように量子コンピュータの計算に応用するのでしょうか?
それは重ね合わせと量子もつれという量子特有の2つの原理を利用することで従来よりはるかに高速な計算の可能性が見出されています。1つずつ見ていきましょう。
重ね合わせ
量子コンピュータではビットの0/1というのは量子の状態で表します。磁石に例えるとS極が上を向いている状態を0、N極が上を向いている状態を1として0/1を表現しています。
ここで、従来のコンピュータではビットの値は必ず0か1かに決定します(電流がONかOFFか)。しかし量子ビットはなんと0でもあり1でもある状態という状態を取ります。これを状態の重ね合わせと言います。

この現象は先ほど紹介した量子が波の性質を持つことに由来します。波は複数の状態の波が同じ場所に共存して影響を及ぼすのでした。そのため波の性質を持つ量子も複数の量子が共存するという現象が起きるのです。
量子の状態は観測して初めてわかる

重ね合わせをわかったけど、でも結局量子の状態は0か1にならないと計算できないじゃん!
その通りです。量子の状態は最終的に0か1かのどちらかです。ではいつ状態が判明するかというと、量子の状態を観測した瞬間に量子の状態が確定します。意味不明ですね。

先ほども書いたように、量子は波として0の状態と1の状態が重ね合わさった状態でいます。そのため私たちの目には見えません。
しかし量子は粒子でもあるので、私たちが量子を粒子として「観測」しようすると途端に波は1点に集まって粒子として振る舞うのです。
つまり量子は状態を観測するまではどちらの状態も取りうるけれど、観測した瞬間量子の状態が確定するということです。これを波束の収縮と言います。
量子もつれ(エンタングルメント)
量子もつれとは複数の量子間に生じる現象で、1つの量子状態が確定すると、他の量子の状態にも影響が及ぶ現象です。
従来のコンピュータでは隣のビットが0から1に変わったからといって自分に影響が及ぶわけはないですよね。しかし量子ビットではそんな現象が起こり得るのです。
重ね合わせと量子もつれの使い道
これらの2つの現象は量子力学の公理と言われ、なぜということが説明できません。そういうモノだとして受け入れるしかないのです。
では重ね合わせと量子もつれによって何が可能になるかというと、一度に何通りもの計算が可能になります。
重ね合わせを利用することで1度に複数の状態を作り出すことが可能です。例えば2つの量子ビットを考えると、それぞれの量子ビットが0と1の2つの状態の重ね合わせを取ることができるため全体では下のように4つの状態が考えられます。
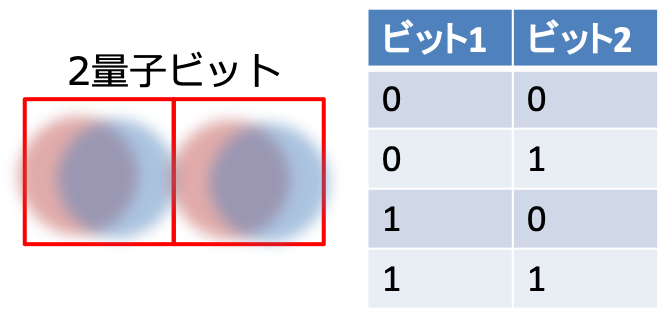
これが10個になると1024通り30個では1073741824通りとなります。重ね合わせを利用することでものすごい数の状態を一度に表現できるのです。この状態で演算を行うことで一度に何通りもの計算が可能となります。
さらに量子もつれを利用することで一方の状態が確定するともう一方の状態も確定する状況を作り出するため計算処理を減らすことができると考えられています。
まとめ
- 量子は粒子と波の両方の性質を持つ。
- 量子には重ね合わせと量子もつれという量子特有の現象が存在する。
- 重ね合わせとは複数の状態が共存して存在することである。
- 量子もつれとは一方の状態が確定するともう一方の状態に影響する現象である。
- 2つの現象は量子コンピュータの高速計算処理において重要な役割を果たす。






コメント