Dynamic Circuitsとは
Dynamic Circuitsとは、量子回路の途中で測定を行い、その結果に応じてその後にかける量子ゲートを動的に変更することを可能とするQiskitの機能です。
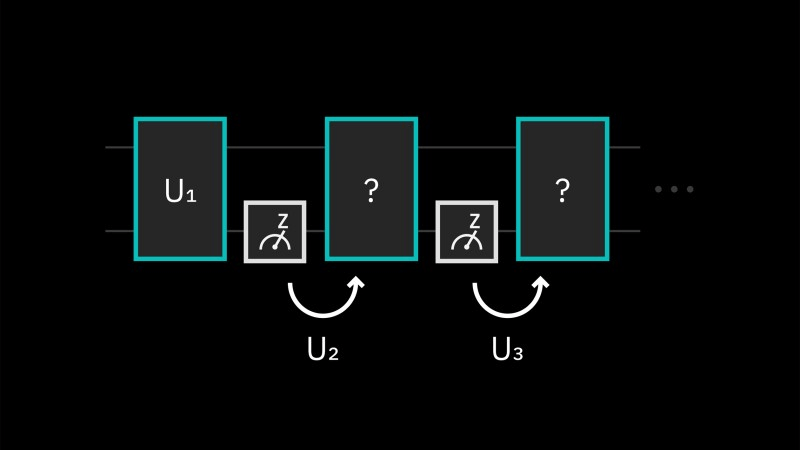
これまでの量子回路(静的回路と呼ぶことにします)では、量子状態を知るための測定操作は必ず回路の最後に行われました。
そのため、回路の途中の量子状態に応じて後続の操作を組み換えるといったフィードフォワード制御はできませんでした。
Dynamic Circuitsがサポートされることで、量子回路設計において次のメリットを受けることが出来ます。
- 量子回路にフィードフォワードを導入できることで、複雑な実装が必要だった静的回路をよりシンプルにする(深さを減らす)ことが出来る。
- 古典計算の”For”や”If/Then”の条件分岐を量子計算に取り入れることが出来る。
この他にもエラー訂正や量子状態の準備、量子機械学習の領域で効果が挙げられていると報告されています。
QiskitでDynamic Circuitsを実装する
Qiskitを使ってDynamic Circuitsの実装を試してみましょう。例題としてIBM Quantum Challenge2023 SpringのLab1の問題を使います。
回路の途中で量子ビットの測定結果に応じて後続操作を組み替える2量子ビット回路を実装します。
実装はif_test()を利用するだけです。量子ビット$q_0$を測定して結果が0なら$q_1$にXゲートを、1ならHゲートを適用するような動的回路を実装してみましょう。
from qiskit import QuantumCircuit
from qiskit.circuit import QuantumRegister, ClassicalRegister
qr = QuantumRegister(2)
cr = ClassicalRegister(2)
qc = QuantumCircuit(qr, cr)
q0, q1 = qr
b0, b1 = cr
qc.h(q0)
qc.measure(q0, b0)
# dynamic circuits
with qc.if_test((b0, 0)) as else_:
qc.x(1)
with else_:
qc.h(1)
qc.measure(q1, b1)
qc.draw(output="mpl", idle_wires=False)量子回路を図示すると下のような回路になります。
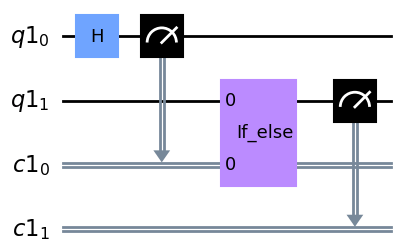
早速実行結果を確認してみましょう。$q_0$が0なら$q_1$は100%の確率で1が出力され、$q_0$が1ならHゲートを適用するので、$q_1$は0と1が50%の確率で出力されるはずです。
つまり、全体では$q_1q_0$が10が50%、11が25%、01が25%で観測されることが期待されます。
from qiskit_aer import AerSimulator
backend_sim = AerSimulator()
job_1 = backend_sim.run(qc)
result_1 = job_1.result()
counts_1 = result_1.get_counts()
print(f"Counts: {counts_1}")
## Counts: {'11': 248, '01': 254, '10': 522}期待通りの結果が出力されました。非常にシンプルな実装でDynamic Circuitsを実現できることが確認できました。
Repeat Until Success!
Dynamic Circuitを利用することで、出力がランダムで測定した結果が間違っていたとしても正しい結果が出るまで回路の実行を繰り返すことが出来ます。
Quantum Challengeではパラメータゲート$R_X(\theta)$を非パラメータゲートを使って再現する量子回路を例として扱っています。
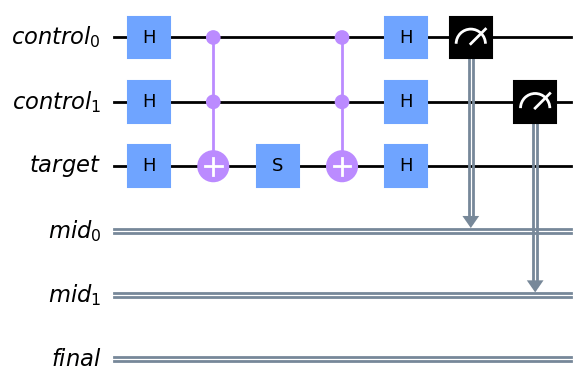
この回路はcontrolとラベルされた量子ビット(以下コントロールビット)が両方0のとき、targetとラベルされた量子ビット(以下ターゲットビット)には$R_X(\theta)$ゲートが適用される回路です。$(\cos\theta=3/5)$
量子回路に存在しない回転ゲートの話がいきなり出てきて戸惑いますが、丁寧に計算してみると理解できます。
まずコントロールビットのみを考えると単純で、最初のアダマールゲートをかけた後の量子状態は以下のように表せます。
|\psi_{control_1}\psi_{control_0}\rangle=\frac{1}{2}(|00\rangle+|10\rangle+|01\rangle+|11\rangle)ここにターゲットビットも加えて計算すると、量子状態は以下のように表せます。(コントロールビットの最後のアダマールゲートをかけるのを忘れずに)
\begin{aligned}
|\psi_{target}\psi_{control_1}\psi_{control_0}\rangle
&=\frac{1}{2}\{HSH|\psi_{target}\rangle\otimes H(|00\rangle+|10\rangle+|01\rangle)
+HXSXH |\psi_{target}\rangle \otimes H |11\rangle\} \\
&=\frac{1}{4}\{
H(3S+XSX)H |\psi_{target}\rangle \otimes |00\rangle + H(S-XSX)H |\psi_{target}\rangle \otimes( |10\rangle+|01\rangle-|11\rangle)\}\\
&=\frac{1}{4}\{\sqrt\frac{5}{2}e^{i\pi/4}R_X(\theta) |\psi_{target}\rangle \otimes |00\rangle + \sqrt2e^{-i\pi/4}X |\psi_{target}\rangle \otimes (|10\rangle+|01\rangle-|11\rangle)\}
\end{aligned}コントロールビットが両方0の時、たしかに$R_X(\theta)$ゲートと同等の処理が行われることが確かめられました。
今回ターゲットビットに$R_X(\theta)$が適用される状態を作り出したいです。そこでDynamic Circuitを使ってコントロールビットの測定値が両方0となるまで繰り返し量子回路を実行させるように設計します。
量子回路の準備
まずは最初にイメージを挙げた量子回路を準備する関数を定義します。
def trial(
circuit: QuantumCircuit,
target: QuantumRegister,
controls: QuantumRegister,
measures: ClassicalRegister,
):
"""Probabilistically perform Rx(theta) on the target, where cos(theta) = 3/5."""
circuit.h(range(3))
circuit.ccx(0,1,2)
circuit.s(2)
# uncomputation
circuit.ccx(0,1,2)
circuit.h(range(3))
circuit.measure(range(2),range(2))リセット処理の定義
コントロールビットがのどちらか1つでも0でない場合、ターゲットビットにはXゲートがかかります。しかし私たちが望む結果は$R_X(\theta)$ゲートがかかった状態なので量子ビットをリセットする必要があります。
def reset_controls(
circuit: QuantumCircuit, controls: QuantumRegister, measures: ClassicalRegister
):
"""Reset the control qubits if they are in |1>."""
with circuit.if_test((measures[0], 1)) as else_:
circuit.x(0)
with circuit.if_test((measures[1], 1)):
circuit.x(1)量子回路全体の構成
必要な処理の部品は定義したので後は全体を組み合わせます。処理の流れは以下の通りです。
trial回路の処理を実行- 2つのコントロールビットを測定→両方0なら終了
- そうでない場合は量子ビットをリセット
- 2以降を繰り返す
Qiskitの制約で現状古典レジスタの値のチェックとループ処理が直接実装出来ないため、最大2回の繰り返しでお茶を濁すこととします。
# Set the maximum number of trials
max_trials = 2
# Create a clean circuit with the same structure (bits, registers, etc)
# as the initial base we set up.
circuit = base.copy_empty_like()
# The first trial does not need to reset its inputs, since the controls
# are guaranteed to start in the |0> state.
trial(circuit, target, controls, mid_measure)
# Manually add the rest of the trials. In the future, we will be
# able to use a dynamic `while` loop to do this, but for now, we
# statically add each loop iteration with a manual condition check
# on each one. This involves more classical synchronizations than
# the while loop, but will suffice for now.
for _ in range(max_trials - 1):
reset_controls(circuit, controls, mid_measure)
with circuit.if_test((mid_measure, 0b00)) as else_:
# This is the success path, but Qiskit can't directly
# represent a negative condition yet, so we have an
# empty `true` block in order to use the `else` branch.
pass
with else_:
circuit.x(target[0])
trial(circuit, target, controls, mid_measure)
# We need to measure the control qubits again to ensure we
# get their final results; this is a hardware limitation.
circuit.measure(controls, mid_measure)
# Finally, let's measure our target, to check that we're
# getting the rotation we desired.
circuit.measure(target, final_measure)
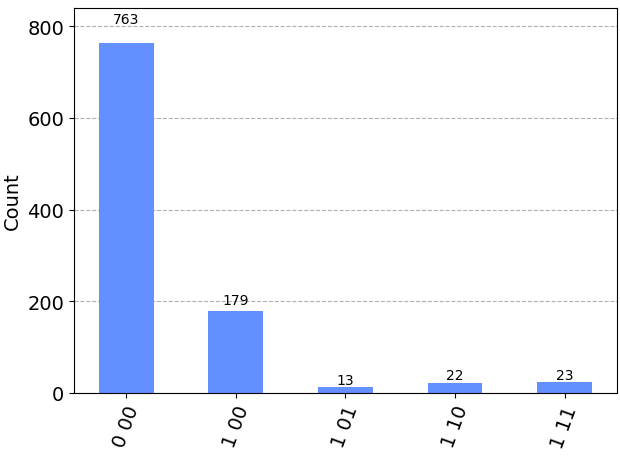
circuit.draw("mpl", cregbundle=False)結果を測定するとコントロールビットが0である確率、つまりターゲットビットに$R_X(\theta)$ゲートが印加されている確率が高くなっていることが確認できます。
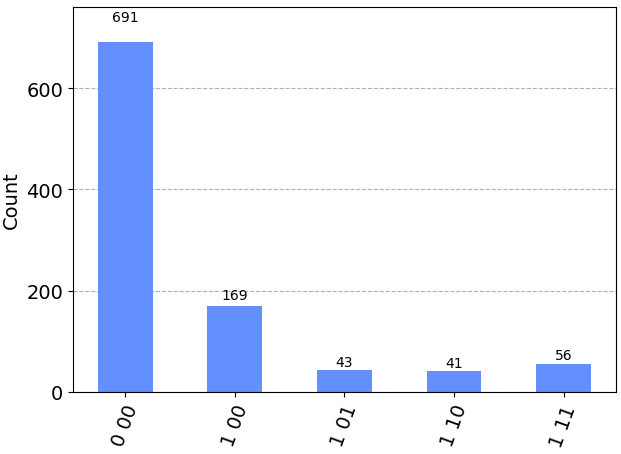
繰り返しを2回から3回にすると望みの状態の確率が高くなったことが確認できます。これを繰り返すと限りなく1に近い確率で$R_X(\theta)$の印加を実現することが出来ます。
まとめ
この記事ではQiskitのDynamic Circuitsの機能の導入について紹介しました。
回路の途中で量子状態を測定して量子回路を組み替えられるというのが非常に大きな特徴ですね。どんな使い方が出来るか他の記事でも紹介していこうと思います。








コメント