現在の量子機械学習の取組みでは、NISQデバイスを前提としてパラメータ化された量子回路による学習モデルが注目されています。
その一つである量子SVMについて、IBM Quantum Challenge 2022 fallで取り上げられた手書き文字の識別モデルの構築について紹介します。
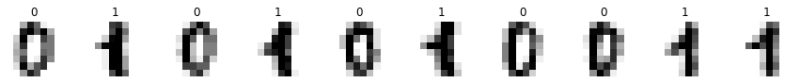
SVM(Support Vector Machine)
SVMは教師あり学習アルゴリズムの1つで、2値分類問題に用いられます。
マージンという分類境界と最も近いデータ点との距離が最大となるように最適化することで、学習モデルに高い汎化性能を持たせます。

決定境界(超平面)に最も近いデータ点はサポートベクトルと呼ばれます。
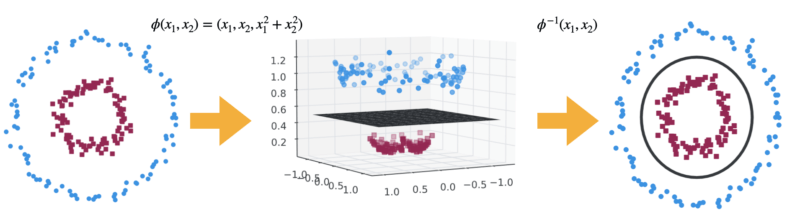
SVMは線形アルゴリズムですが、カーネル化することで非線形分類問題へのアプローチが容易になります。
カーネルの詳細はこちらで解説しているので省きますが、線形分離可能な高次元空間へ射影して学習モデルを構築する手法です。
量子SVM
量子SVMはカーネル化したSVMをベースとした量子・古典ハイブリッドアルゴリズムです。
カーネルと量子計算の構造がよく似ているためカーネルの計算に量子コンピュータを用います。
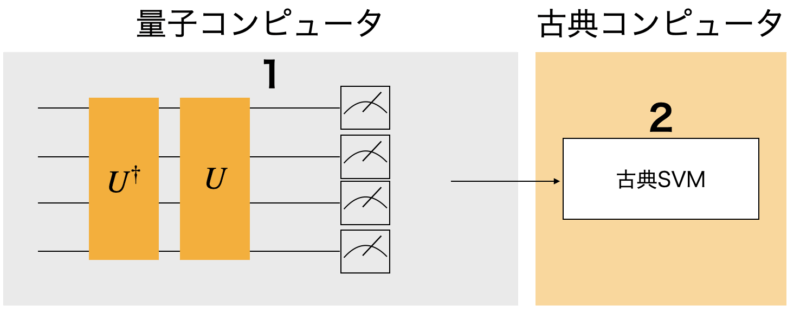
量子SVMアルゴリズムの手順は以下の通りです。
- 訓練データとテストデータからカーネルを量子計算で求める。
- 上で求めたカーネルを用いて古典SVMで学習モデルを構築する。
手書き文字識別モデルを構築する
では量子SVMの学習モデルを構築してみましょう。IBM Quantum Challenge 2022 fallを題材に、scikit-learnの手書き文字データセットを使用します。
問題では以下のようなサンプル25個を訓練データ、10個をテストデータとして使用しています。
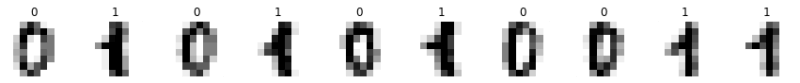
データ符号化回路を構築する
最初にカーネル計算のための核となる古典データを量子状態へ符号化する回路$U$を構築します。
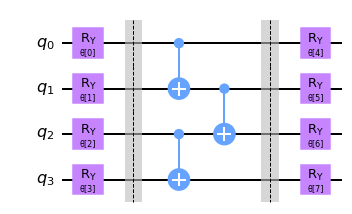
データ符号化の方法は様々ありますが、問題ではRealAmplitude回路を用いて古典データを量子状態の振幅に符号化しています。
from qiskit.circuit.library import RealAmplitudes
def lab2_ex1():
qc = RealAmplitudes(4, reps=1, entanglement='pairwise', insert_barriers=True)
return qc
qc = lab2_ex1()
qc.decompose().draw('mpl')カーネルを計算する
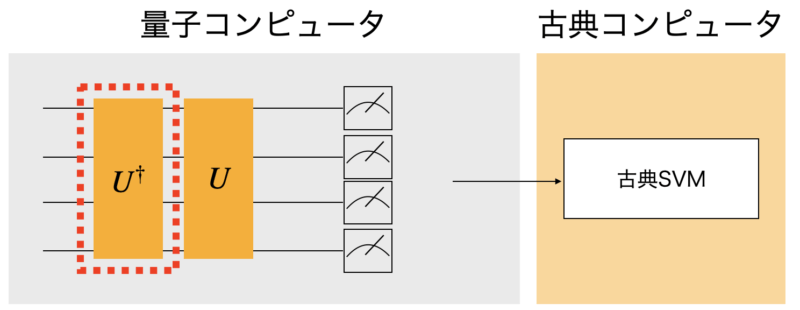
カーネルを計算する回路はデータ符号化回路$U$に対して$U^\dagger U$となります。
\begin{aligned}
\kappa(\bm{x^{m}},\bm{x^{m'}}) = |\langle\Phi(\bm{x^{m}})|\Phi(\bm{x^{m'}})\rangle|^2 \\
= |\langle0|^{\otimes N}U^\dagger U|0\rangle^{\otimes N}|^2 \\
\end{aligned}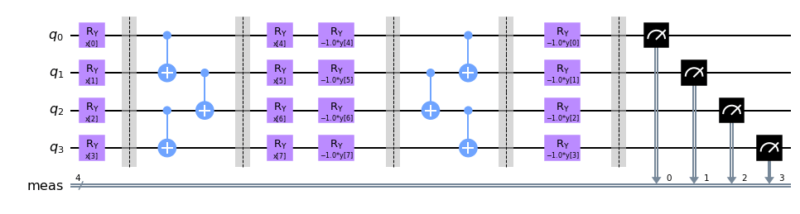
問題のPart4では教育観点から回路の構築から計算をスクラッチで行っていますが、実際の利用ではQiskit Machine Learningモジュールを利用します。
from qiskit_machine_learning.kernels import FidelityQuantumKernel
feature_map=RealAmplitudes(4, reps=1, entanglement='pairwise', insert_barriers=True)
kernel = FidelityQuantumKernel(feature_map=feature_map)
K = kernel.evaluate(sample_train)
plot_matrix(K, 'kernel matrix (em)')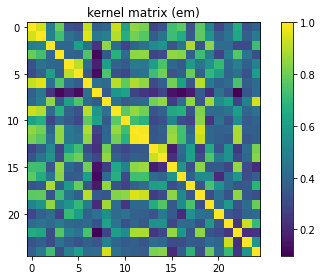
SVMアルゴリズムを実行する
最適化計算の部分は古典機械学習と全く同じです。量子計算で求めたカーネルを使ってSVMを実行することで正確な分類器を構築することができました。
svc = SVC(kernel='precomputed')
# train SVM
svc.fit(K, labels_train)
# score SVM on training data
y_predict = svc.predict(K)
print('accuracy (sim):', sum(y_predict == labels_train)/len(labels_train))
### accuracy (sim): 1.0まとめ
この記事ではIBM Quantum Challenge2022 fallを題材として量子SVMによる手書き文字の認識モデルを構築しました。
ここで量子SVMはパラメータ化された量子回路を使ったアプローチが唯一ではないことは覚えておいてください。
他のアルゴリズムも同様ですが、古典手法を量子計算で高速化する取組みは様々な手法が提案されているので混乱しないようにしてください。








コメント