量子コンピュータのアルゴリズムを勉強しているとQAOAという手法をよく見かけますが、量子回路の仕組みを理解するのはなかなか難しいですよね。

この記事ではQAOAアルゴリズムの基礎として量子回路の成り立ちについて紹介します。
QAOAアルゴリズムとは
QAOA(Quantum Approximate Optimization Algorithm)とは組み合わせ最適化問題をエネルギー最小化問題として解決するためのアルゴリズムです。
NISQアルゴリズムとして量子計算による高速化は保証されないものの、シンプルな構造を持ち現状のハードウェアでも実行が可能です。
NISQとはNoisy Intermediate-Scale Quantumの略称で、現状の小規模な量子コンピュータを指します。
量子誤り訂正がなく計算能力も限定的ですが、何か役に立たないかという観点でNISQアルゴリズムの研究が盛んに行われています。
QAOAのベースとなるアイデアは量子断熱計算
具体的な量子回路の構造を説明する前に、QAOAのベースとなっている量子断熱計算という考え方を理解しましょう。
量子断熱計算とは、問題の解が物理系のハミルトニアン$H$の基底状態であるときに、自然現象を使って初期状態から解となる基底状態を得る手法です。
この手法は量子アニーリングと共通点が多く、代表例であるD-Waveマシンは同じように自然現象の量子効果を使って最適化問題を解くように実装されています。


量子断熱計算が組み合わせ最適化問題とどう関係しているのよ…
という疑問が浮かぶと思いますが、実は下のような関係でつなげることが出来るのです。
- 組み合わせ最適化問題を数理モデル化
- 数理モデルと数学的に等価な物理系がある場合、物理系の振る舞いがわかれば数理モデルの解も求めることができる。
- 数理モデルの最適化はコスト関数を最小化する問題とみなすことができ、対応する物理系ではエネルギー最小化問題(系の基底状態を求める)と読み替える事ができる。
- 系の基底状態を計算する手法の1つである量子断熱計算を採用することで解を求めることができる。
つまり、組み合わせ最適化問題を数理モデル化したときに、数学的に等価な物理系と対応させることができれば量子断熱計算を利用することで解を求めることが出来るということです。
最適化問題の多くはQUBOという数理モデルで表すことができ、これはイジングモデルという物理系と等価であることが知られています。
QUBOとイジングモデルの関係については下の記事を参考にしてください。
QAOAアルゴリズムの量子回路の仕組みを理解する
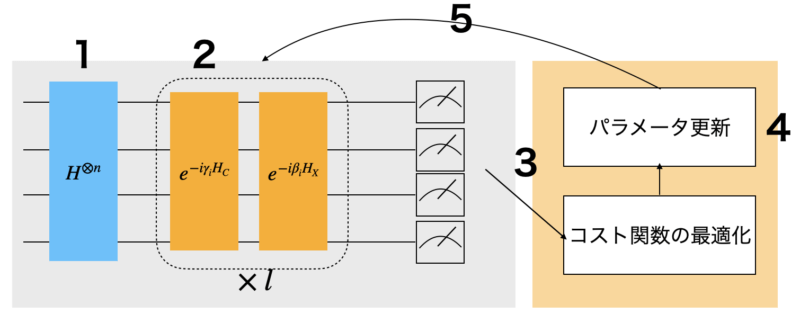
ベースの考え方を理解したところで本題の量子回路の仕組みに移りましょう。まずQAOAアルゴリズムは以下の手順で計算されます。
- 初期状態$|s\rangle=|+\rangle^{\otimes n}$を用意する。
- パラメータ$\beta_i$と$\gamma_i$を持つユニタリゲート$U_C(\gamma_i)=e^{-i\gamma_iH_C}$と$U_X(\beta_i)=e^{-i\beta_iH_X}$を$|s\rangle$に作用させて状態$|\beta, \gamma\rangle$を得る。
- 量子コンピュータで期待値$\langle \beta, \gamma|H_C|\beta, \gamma\rangle$を測定する。
- 古典コンピュータで期待値を小さくする方向へパラメータを更新する。
- 最適解$\beta^*, \gamma^*$が求まるまで1~4を繰り返す。
- 最適化されたパラメータの状態$|\beta^*, \gamma^*\rangle$を測定して妥当な結果を解として出力する。
アルゴリズムの全体像は以下のようになります。
初期状態の準備
初期状態$|s\rangle$および初期ハミルトニアン(ミキサハミルトニアンとも呼びます)$H_X$は決まったものである必要は無く、効率的な計算となる適切なものを用意できればよいです。
一般的には初期ハミルトニアンは$X$ゲートとその固有状態の$|+\rangle$が利用されます。
H_X=\sum^n_{j=1}X_jユニタリゲートの構築
量子断熱計算を行う量子ゲートを構築します。量子断熱計算ではハミルトニアンは下のように表すことができます。
H(t)=(1-\frac{t}{T})H_X+\frac{t}{T}H_C状態の時間発展はシュレーディンガー方程式から計算することができます。
この計算は全体の時間$T$を微小区間$\Delta t$に分け、その範囲でハミルトニアンは一定であると近似することで手法がよくとられます。
\begin{aligned}
|\psi(t)\rangle&=e^{iH(t)t}|s\rangle \\
&= e^{i\Delta tH(T,T-\Delta t)}e^{i\Delta tH(T-\Delta t, T-2\Delta t,)}\cdots e^{i\Delta tH(\Delta t, 0)}|s\rangle \\
&=\Pi_j e^{i\Delta tH(j\Delta t, (j+1)\Delta t)}|s\rangle \\
&=\Pi_j e^{-i\beta_jH_X}e^{-i\gamma_jH_C}|s\rangle
\end{aligned}計算式を変換していくことでアルゴリズムの説明で登場したパラメータを2つもった量子ゲートが必要な理由がわかりました。
エネルギー最適化問題の計算
アルゴリズムの手順3以降は問題の数理モデルと対応する物理系のハミルトニアン$H_C$のエネルギー最小化問題の計算を行っています。
この部分は他のアルゴリズムと共通でハミルトニアンの期待値$\langle \beta, \gamma|H_C|\beta, \gamma\rangle$からエネルギーがわかるので最小化するようにパラメータを調整するという手順となります。
まとめ
この記事ではQAOAアルゴリズムの量子回路の構造について、ベースの量子断熱計算のアイデアを踏まえて紹介しました。
詳細はこちらの参考文献を勉強するとより理解が深まります。量子コンピュータを勉強する方はぜひ一読することをおすすめします。










コメント