位相キックバックという言葉を聞いたことあるでしょうか?
意外とこんな方が多いのではないでしょうか?

単語は聞いたことあるけどいまいち意味は理解していない

位相キックバックなんて全く聞いたことがない
量子コンピュータを参考書などの始めの方に登場する用語ですが、位相キックバックについては触れられているものの、何が位相キックバックなのかという説明はされてない場合が多いと思います。
そこでこの記事では位相キックバックとは何か、そしてなぜ重要なのかを紹介します。
位相キックバックとは
位相キックバックとは制御演算(CNOTなど)において、標的ビットに作用するゲートの固有値が制御ビットの位相に反映させる量子演算のテクニックを指します。
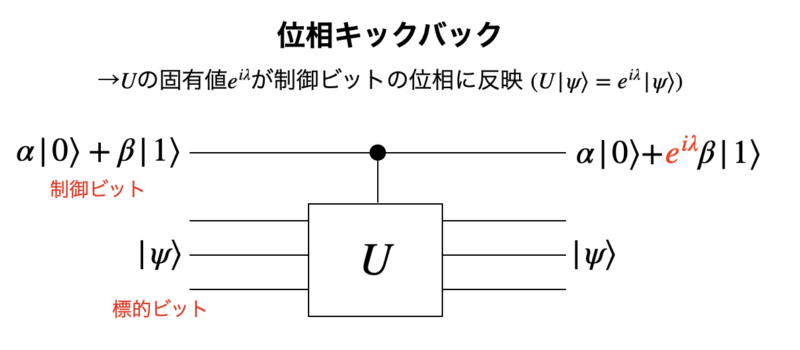
具体的な例で確認します。$| +-\rangle$に対してCNOTゲート操作をする場合を考えます。
\begin{aligned}
CNOT|+-\rangle
&= \frac{1}{\sqrt{2}}(| 0\rangle + | 1\rangle) \otimes | -\rangle \\
&=\frac{1}{\sqrt{2}}(| 0\rangle \otimes | -\rangle + | 1\rangle \otimes X| -\rangle) \\
&=\frac{1}{\sqrt{2}}(| 0\rangle \otimes | -\rangle - | 1\rangle \otimes | -\rangle) \\
&= \frac{1}{\sqrt{2}}(| 0\rangle \textcolor{red}{-} | 1\rangle) \otimes | -\rangle \\
&= |--\rangle
\end{aligned}注目したいのは、CNOTゲートの制御操作によって標的ビット$|-\rangle$にXゲートが印加されたにも関わらず、標的ビットの状態は変化せずに制御ビットの位相が変化したという点です。
さらに標的ビットの位相は標的ビット$|-\rangle$に対するXゲートの固有値-1分だけ変化している事がわかります。
位相キックバックはほぼ全ての量子アルゴリズムに使われる
このように位相キックバックは制御操作によって、標的ビットの状態を変えずにゲートの固有値を制御ビットの位相に反映させる点が大きな特徴です。
標的ビットを演算に使用したい量子ビット、制御ビットを補助ビットとみなせば量子ビットの状態を変えずにゲートの固有値情報を取り出せるのは魅力的です。
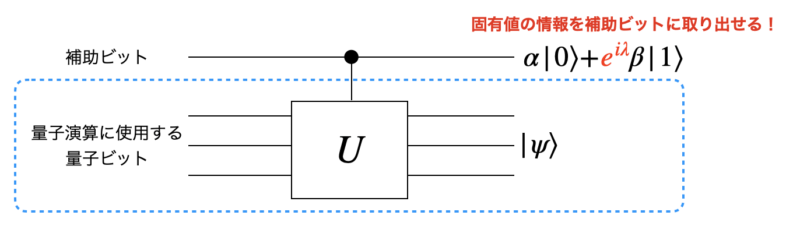
実は位相キックバックのテクニックはほとんど全ての量子アルゴリズムに利用されています。
位相キックバックによってゲートの固有値を位相に反映させ、位相を操作するテクニックを利用して位相中の固有値情報を測定可能にすることで行列の固有値を取り出すことが可能となるため、非常に多くの場面で利用されています。
位相キックバックを利用する際の注意
実際に量子アルゴリズムにおいて位相キックバックを利用する際には以下の前提を満たしている必要があることに注意が必要です。
- 制御ビットは重ね合わせの状態である
- 標的ビットはユニタリ演算の演算子$U$の固有状態である
これら2つの前提は全く突飛なものではありません。それぞれの前提を考えていきます。
制御ビットは重ね合わせの状態である
制御ビットが重ね合わせの状態出ない場合を考えると簡単です。
冒頭のCNOTの例は$| +-\rangle$に対する操作を考えましたが、$|x-\rangle$(x={0, 1})に対する操作を考えてみましょう。
CNOT|x-\rangle =
\begin{cases}
|0-\rangle &\text{ if } x=0 \\
-|1-\rangle &\text{ if } x=1
\end{cases}$x=0$の場合はそもそも演算が実行されないため状態に変化はなく、$x=1$の場合でもゲートの固有値-1はグローバル位相としてかかるため、観測できない(意味のある情報として利用できない)のです。
標的ビットはユニタリ演算の演算子$U$の固有状態である
こちらの前提も標的ビットが演算子$U$の固有状態でない場合を考えると簡単です。
同じ例として、適当な標的ビット$|\psi\rangle$を持ち出してCNOT演算をする場合を考えましょう。
\begin{aligned}
CNOT|+\psi\rangle
&= \frac{1}{\sqrt{2}}(| 0\rangle + | 1\rangle) \otimes | \psi\rangle \\
&=\frac{1}{\sqrt{2}}(| 0\rangle \otimes | \psi\rangle + | 1\rangle \otimes X| \psi\rangle) \\
\end{aligned}ここから先に進めなくなってしまいます。冒頭の例では標的ビットの$|-\rangle$はCNOTゲートの制御演算子$X$の固有状態であったため位相キックバックとして利用することが出来ましたが、固有状態出ない場合は上手くいかない点に注意が必要です。
まとめ
この記事では位相キックバックの概要とその重要性について説明しました。
本文中でも言いましたが、位相キックバックのテクニックはほぼすべての量子アルゴリズムの1ステップとして取り入れられています。
一度そのような観点で今勉強しているアルゴリズムを見直してみてはいかがでしょうか!








コメント