主成分分析(PCA:Principal Component Analysis)とは次元の高い(特徴量の多い)データセットの情報を要約し、少ない特徴量で元の情報を表現する特徴抽出の手法です。
主成分分析は線形回帰やSVMなどのような教師あり学習のアルゴリズムとは異なり、教師なし学習にあたります。
教師なし学習とは
そもそも教師なし学習は何のために使われるかというと、主に前処理の段階で手元のデータ構造を把握するために使われます。
教師なし学習は教師データを用いて学習を行わないため未来の予測には向きませんが、既知のデータ構造を理解する上では非常に有用です。そのため教師なし学習の目的としては以下の2点が挙げられます。
- 分析者のデータ理解をより高める
- 前処理の効果を高めて教師あり学習アルゴリズムの性能を向上させる
データを要約する新たな座標軸を見つける
本記事では主成分分析の目的を大雑把に理解することが目標です。
主成分分析の目的とはデータを要約する新しい座標軸を見つけることです。
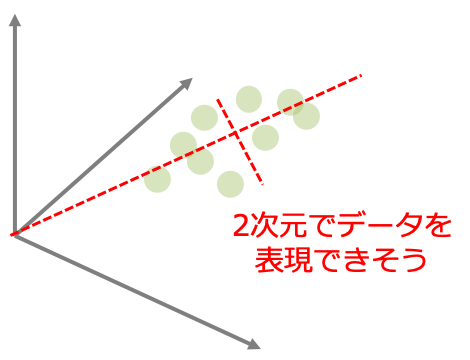
例えば特徴量が3つあるデータが特徴空間内で上のように分布しているとしましょう。よく見るとこれらのデータ点は赤い点線の2本の座標軸でも情報を表現できると考えられます。
これが主成分分析の考え方です。3次元の情報に対して新しい座標軸(主成分)を設定することで次元を落として情報を表現する手法です。
ではどのように座標軸を見つけるのかというと、データの分散が最大となる座標軸を探していきます。教師あり学習がデータの法則性を見つけるためにはデータにばらつき(分散)が必要となります。つまり「情報=ばらつき」なのです。
分散を最大化する座標軸の決定方法は共分散行列という行列を使った数学を必要とするため別の記事で紹介します。
まとめ
- 主成分分析はデータを要約する特徴抽出の手法である
- 主成分分析は教師なし学習の一つでデータの構造理解に用いられる
- データの要約は分散が最大となるような新しい座標軸を探すことである






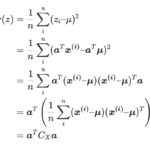
コメント