予測性能の良いモデルを構築するためにはモデルの検証は大切だという話をしました。
今回は検証するモデルをチューニングしてより予測性能を向上させるグリッドサーチ(Grid Search)という手法を紹介します。
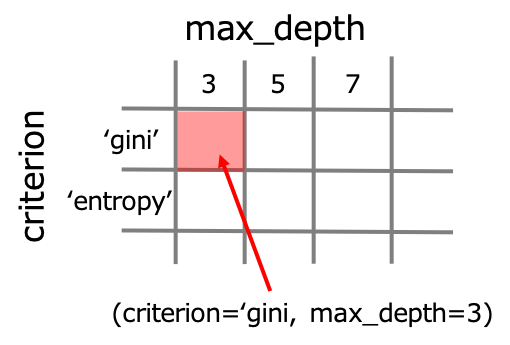
グリッドサーチとは決定木の深さ(max_depth)など私たちが指定するパラメータであるハイパーパラメータの取りうる全ての組み合わせを検証して最適化する手法です。
グリッド(碁盤の目)+サーチ(探索)の名前の通り、下のように碁盤の目のようにハイパーパラメータの組み合わせを一つ一つ検証するイメージです。
それではグリッドサーチをscikit-learnで実装していきます。
データの分割
まずはデータセットを訓練データとテストデータに分割します。
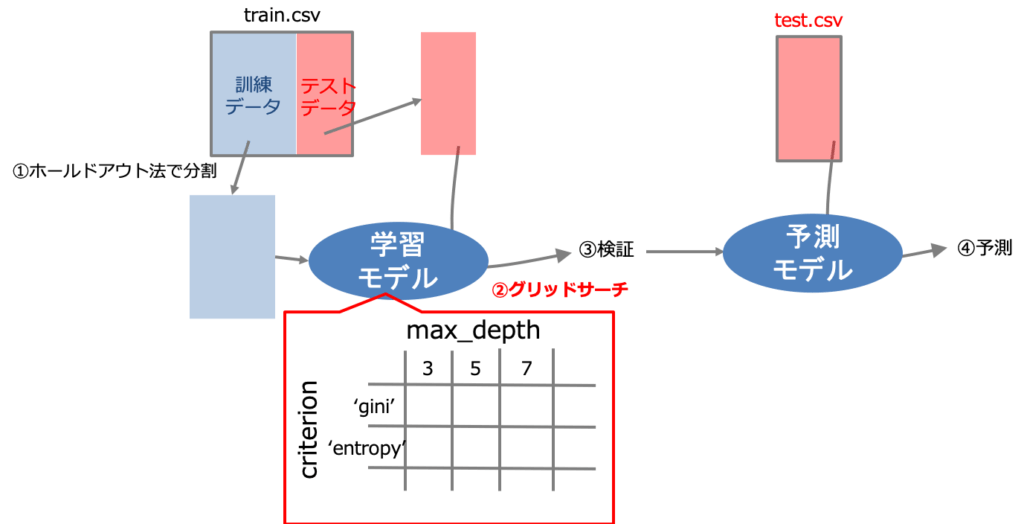
というのも、kaggleなどで配布されるテストデータ(test.csv)は実際には将来手に入る未知のデータです。そのため予測モデルを構築する段階では実際の予測では存在しません。
つまり手元にある訓練データで学習モデルを構築する必要があります。性能の良いモデルを構築するためには検証過程が必須です。なのでデータを分割して検証用のデータを作る必要があるのです。
scikit-learnでグリッドサーチを実装する
使うデータはIrisデータを使用します。

Irisデータって何ですか?
っていう人はこちらの記事をご覧ください。
データを読み込みデータを分割する
#Irisデータセットを読み込む from sklearn import datasets iris = datasets.load_iris() X = iris.data[:, :2] #特徴量は最初の2つを使う y = iris.target #訓練データとテストデータに分割する from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, stratify=y, random_state=1)
In [2]:
#決定木モデルのインスタンスを作成する from sklearn.tree import DecisionTreeClassifier dtc = DecisionTreeClassifier()
グリッドサーチを行う
#グリッドサーチに必要なパラメータグリッドを作成
param_grid = {'criterion' : ('gini', 'entropy'), 'max_depth' : list(range(3, 9, 1))}
#モデルの分割方法を指定(5分割)
from sklearn.model_selection import StratifiedKFold
kf_5 = StratifiedKFold(n_splits=5, shuffle=True, random_state=0)In [4]:
#グリッドサーチのインスタンスを作成(Grid Search Cross Validation) from sklearn.model_selection import GridSearchCV gs = GridSearchCV(dtc, param_grid, cv=kf_5)
In [5]:
#グリッドサーチ推定器を学習 gs.fit(X_train, y_train)
Out[5]:
GridSearchCV(cv=StratifiedKFold(n_splits=5, random_state=0, shuffle=True),
error_score='raise-deprecating',
estimator=DecisionTreeClassifier(class_weight=None,
criterion='gini', max_depth=None,
max_features=None,
max_leaf_nodes=None,
min_impurity_decrease=0.0,
min_impurity_split=None,
min_samples_leaf=1,
min_samples_split=2,
min_weight_fraction_leaf=0.0,
presort=False, random_state=None,
splitter='best'),
iid='warn', n_jobs=None,
param_grid={'criterion': ('gini', 'entropy'),
'max_depth': [3, 4, 5, 6, 7, 8]},
pre_dispatch='2*n_jobs', refit=True, return_train_score=False,
scoring=None, verbose=0)ベストスコアのパラメータの組み合わせを知りたい
#ベストスコアのパラメータの組み合わせを表示 gs.best_params_
Out[6]:
{'criterion': 'gini', 'max_depth': 5}ここからジニ不純度で決定木の深さが5のモデルの予測性能が最も良いことがわかりました。
(補足)全ての組み合わせの結果を確認
#試行結果とスコアを表示
params = gs.cv_results_['params']
means = gs.cv_results_['mean_test_score']
for param, mean in zip(params, means):
print(param, mean)Out[7]:
{'criterion': 'gini', 'max_depth': 3} 0.7583333333333333
{'criterion': 'gini', 'max_depth': 4} 0.7583333333333333
{'criterion': 'gini', 'max_depth': 5} 0.7666666666666667
{'criterion': 'gini', 'max_depth': 6} 0.7333333333333333
{'criterion': 'gini', 'max_depth': 7} 0.725
{'criterion': 'gini', 'max_depth': 8} 0.6916666666666667
{'criterion': 'entropy', 'max_depth': 3} 0.7166666666666667
{'criterion': 'entropy', 'max_depth': 4} 0.7166666666666667
{'criterion': 'entropy', 'max_depth': 5} 0.7166666666666667
{'criterion': 'entropy', 'max_depth': 6} 0.7333333333333333
{'criterion': 'entropy', 'max_depth': 7} 0.6916666666666667
{'criterion': 'entropy', 'max_depth': 8} 0.6916666666666667決定木の深さ(3から8)と不純度(ジニ不純度と情報エントロピー)の全ての組み合わせについて計算が行われています。
ランダムサーチで計算量を節約する
グリッドサーチはあらゆるパラメータの組み合わせを試すため計算量が多くなってしまうことが難点です。そこで使われる手法はランダムサーチと呼ばれる手法です。実装方法はグリッドサーチとほとんど同じです。
#決定木モデルのインスタンスを作成する
from sklearn.tree import DecisionTreeClassifier
dtc = DecisionTreeClassifier()
#ランダムサーチに必要なパラメータ分布を作成
param_dist = {'criterion' : ('gini', 'entropy'), 'max_depth' : list(range(3, 9, 1))}
#ランダムサーチのインスタンスを作成
from sklearn.model_selection import RandomizedSearchCV
rs = RandomizedSearchCV(dtc, param_dist, cv=kf_5, n_iter=6) #n_iter:繰り返し回数In [9]:
#ランダムサーチ推定器を学習させる rs.fit(X_train, y_train)
Out[9]:
RandomizedSearchCV(cv=StratifiedKFold(n_splits=5, random_state=0, shuffle=True),
error_score='raise-deprecating',
estimator=DecisionTreeClassifier(class_weight=None,
criterion='gini',
max_depth=None,
max_features=None,
max_leaf_nodes=None,
min_impurity_decrease=0.0,
min_impurity_split=None,
min_samples_leaf=1,
min_samples_split=2,
min_weight_fraction_leaf=0.0,
presort=False,
random_state=None,
splitter='best'),
iid='warn', n_iter=6, n_jobs=None,
param_distributions={'criterion': ('gini', 'entropy'),
'max_depth': [3, 4, 5, 6, 7, 8]},
pre_dispatch='2*n_jobs', random_state=None, refit=True,
return_train_score=False, scoring=None, verbose=0)In [10]:
#ベストスコアのパラメータの組み合わせを表示 rs.best_params_
Out[10]:
{'max_depth': 4, 'criterion': 'gini'}グリッドサーチの結果と比較するとベストなモデルのパラメータは不純度については一緒となり、木の深さについては1異なる(4と5)結果が得られました。
In [11]:
#試行結果とスコアを表示
params = rs.cv_results_['params']
means = rs.cv_results_['mean_test_score']
for param, mean in zip(params, means):
print(param, mean)Out[11]:
{'max_depth': 4, 'criterion': 'gini'} 0.7666666666666667
{'max_depth': 6, 'criterion': 'gini'} 0.7333333333333333
{'max_depth': 4, 'criterion': 'entropy'} 0.7166666666666667
{'max_depth': 8, 'criterion': 'gini'} 0.7
{'max_depth': 7, 'criterion': 'entropy'} 0.6916666666666667
{'max_depth': 3, 'criterion': 'entropy'} 0.7166666666666667
In [14]:
#ランダムサーチの実行時間 %timeit rs.fit(X_train, y_train) ==> 24.5 ms ± 660 µs per loop (mean ± std. dev. of 7 runs, 10 loops each) #グリッドサーチの実行時間 %timeit gs.fit(X_train, y_train) ==> 48.4 ms ± 3.51 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
この結果からランダムサーチは半分の実行時間で全ての組み合わせを試す場合と近い結果を得ることができました。グリッドサーチとランダムサーチのどちらを使うかは場合によって異なりますが、まずアルゴリズムが機能するかの感触をつかみたい場合にはランダムサーチは有効と言えます。
まとめ
- 性能の良いモデルを構築するにはグリッドサーチによるハイパーパラメータの調整が有効
- グリッドサーチは全てのパラメータの組み合わせを交差検証する
- 計算量の節約のためにランダムサーチが使われることも多い







コメント