学習モデルを構築して学習させてみると、訓練データに対しては予測性能が90%以上のスコアを出しているのにテストデータに対しては60%程度のスコアしか出ないような過学習の状態がよく起こります。
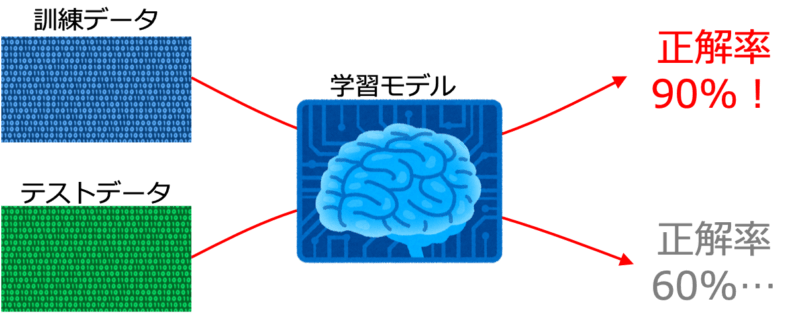
過学習は様々な原因で起こりますが、一つの原因として学習させる特徴量が多すぎてモデルが複雑になりすぎている可能性があります。
過学習を抑える手法として特徴量の数を減らす次元削減という方法が取られます。次元削減には大きく分けて二つの手法が採用されています。
- 特徴選択:手元のデータセットから有益な特徴量だけを選択する
- 特徴抽出:データセットを要約するような新しい特徴量を作り出す
なぜ次元削減をするのか
そもそも私たちはなぜ次元削減をする必要があるのでしょうか。理由としては主に2つです。
次元の呪いを回避する
機械学習においてデータの次元が大きくなりすぎるとデータが表現できる組み合わせが多くなりすぎてしまい手元のデータ数では表現しきれず学習が上手く行えないという問題が起こります。これを次元の呪いと言います。
次元削減をすることによって手元のデータ数でも上手く学習が行えるようにすることが大きな目的の一つです。
意味を捉えやすくする
私たちは物事の因果関係を知るためには登場人物が少ない方が出来事を把握しやすいです。
特に2次元、3次元ではグラフなどの視覚化が可能で、データの構造や予測結果の意味を理解しやすくなります。一方で4次元以上の高次元データでは可視化ができないため意味解釈性が下がります。
そのため私たちは次元削減によってなるべくデータの意味を捉えやすくしようという目的があるのです。
特徴選択のアルゴリズムとしては主に3つの手法があります。
- フィルター法:学習を伴わず特徴量の重要度から選択する
- ラッパー法:学習を行いながら重要な特徴量を選択する
- 埋め込み法:学習アルゴリズムに特徴選択が埋め込まれている
特徴抽出
特徴抽出はデータの要約を行う操作です。データの要約とは実際に観測されている変数(観測変数)から実際には直接観測できないが現象の本質をついている変数(潜在変数)を表現することです。
例えば「学力」を考えましょう。

私たちは学力そのものを直接測定することはできません。しかし受験において学力は大体5科目のテストの合計点(または偏差値)で測られています。世間には高校や大学の偏差値表みたいなものがあるくらいなのだから納得していただけると思います。
つまり各テストの得点という5つの観測変数の情報を、学力という本質的な1つの潜在変数にまとめることができたのです。これがデータの要約です。
学力 = 数学の得点 + 英語の得点 + 国語の得点 + 理科の得点 + 社会の得点
実際の特徴抽出の主な方法としては以下の3つがあります。
- 主成分分析(PCA)
- 線形判別分析
- カーネル主成分分析







コメント