初心者が深層学習を学び始めると、

深層学習ってライブラリで勝手に計算して答え出してくれるけど、結局何をやってるの?
といったことを必ず思う日が来るのではないでしょうか?深層学習って中で何をしているのか全くわからないですよね。
そこで深層学習の簡単な理論側面を理解すること、実際にkerasなどのライブラリを使わずに自分で深層学習モデルを実装することを目標に記事を書いていきます。
全体像を把握する
まずは私たちがこれから学ぶことの全体像を確認しましょう。
このシリーズ記事における私たちのゴールは手書き文字(MNIST)を認識するニューラルネットワークの動作原理を学び、自分たちで実装することです。
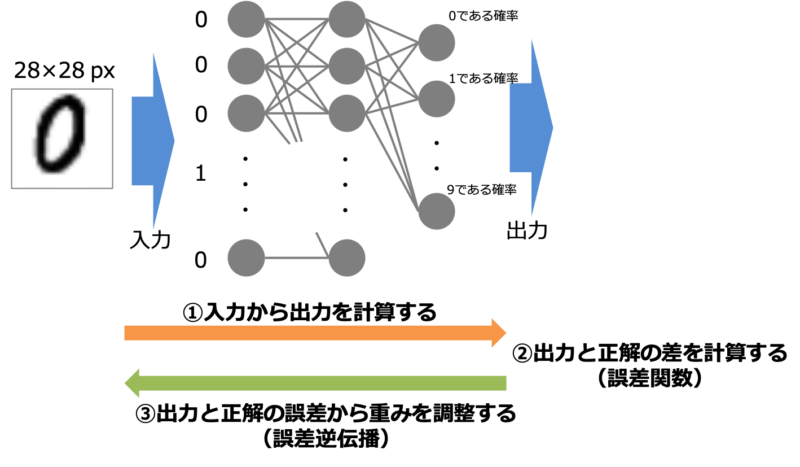
まずは深層学習の最も基本となるニューラルネットワークの動作原理について学びます。何を理解すれば良いかと言うと下の3つの流れです。
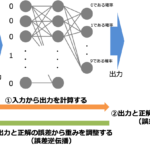
- 入力から出力を計算する(順伝播計算)
- 出力と正解の差を計算する(誤差関数)
- 出力と正解の差が最小となるように重みを調整する(誤差逆伝播)
本記事では上の2つについて紹介します。
出力の計算
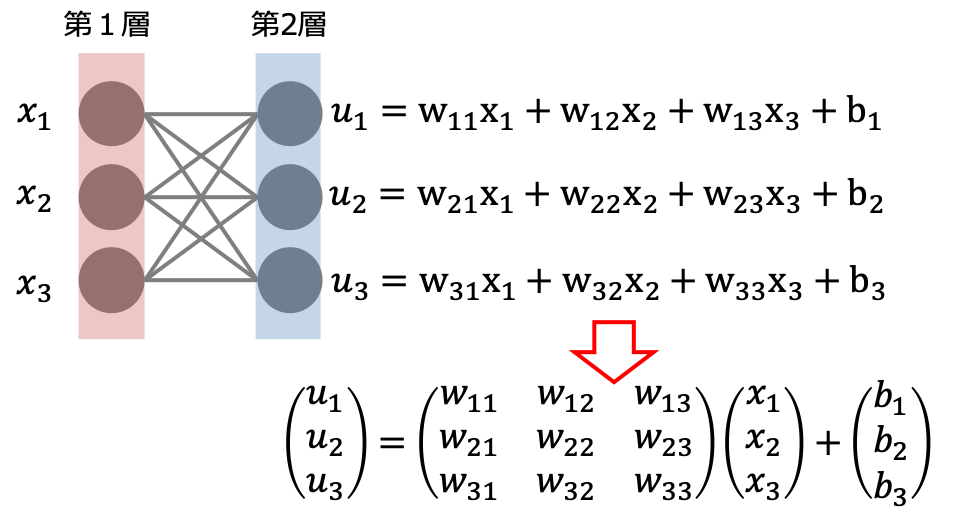
ニューラルネットワークを構成するユニットは前の層のユニットから入力を受けて出力を計算します。
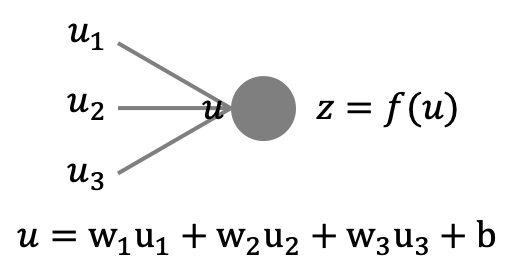
例えば上のように3つのユニットから入力を受ける場合の総入力は
$$w = w_1x_1 + w_2x_2 + w_3x_3 + b$$
のように各入力に重み$w_i$をかけたものにバイアス$b$を足したものとなります。そしてユニットは入力に対して活性化関数$f$に対する出力を返します。つまり入力$w$に対する出力$z$は次のようになります。
$$z = f(u)$$
ニューラルネットワークでは各層に複数のユニットが存在し、各ユニットにおいて同様の計算が行われます。
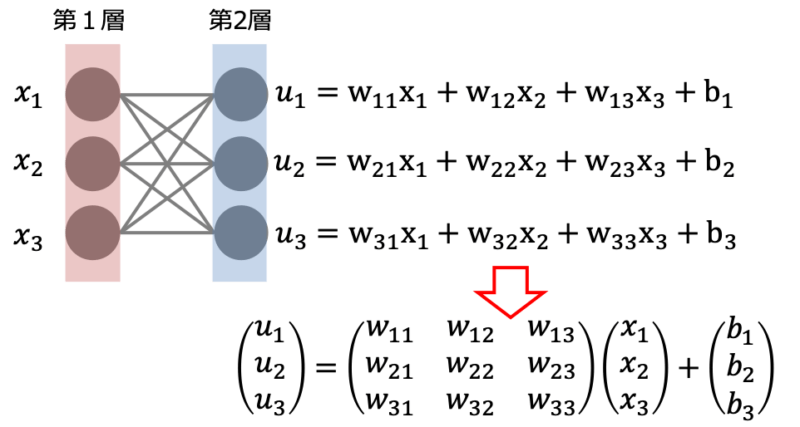
各層の入力出力の関係は上の計算を一般化して行列とベクトルを用いると下のように表すことができます。
$$\begin{aligned}\bf{u} &= \bf{w}\bf{x} + \bf{b} \\ \bf{z} &= f(\bf{u})\end{aligned}$$
多層ニューラルネットワークの計算
今の計算を多層のニューラルネットワークに拡張します。といっても計算は先ほどと変わりません。
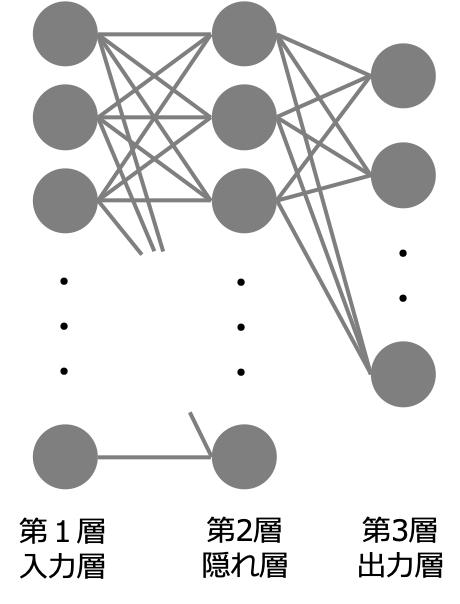
$L$層(図は$L=3$)のニューラルネットワークを考えると、$l=1$の入力層から$l=2$の隠れ層への入力出力関係は次のように表すことができます。(右上の数字は層の番号)
$$\begin{aligned}\bf{u}^{(2)} &= \bf{w}^{(2)}\bf{x} + \bf{b}^{(2)} \\ \bf{z}^{(2)} &= f(\bf{u}^{(2)})\end{aligned}$$
次に$l=2$の隠れ層から$l=3$の出力層への入力出力関係は次のように表すことができます。
$$\begin{aligned}\bf{u}^{(3)} &= \bf{w}^{(3)}\bf{x}^{(2)} + \bf{b}^{(3)} \\ \bf{z}^{(3)} &= f(\bf{u}^{(3)})\end{aligned}$$
以上を一般化して第$l$層から第$l+1$層への入力出力関係は
$$\begin{aligned}\bf{u}^{(l+1)} &= \bf{w}^{(l+1)}\bf{x}^{(l)} + \bf{b}^{(l+1)} \\ \bf{z}^{(l+1)} &= f(\bf{u}^{(l+1)})\end{aligned}$$
のように計算することができます。この時入力層の出力を$\bf{z}^{(1)}=\bf{x}$、最終的な出力は$\bf{z}^{(L)}=\bf{y}$と表記することにします。(プログラム上では入力はx、出力をyと表記することが多いため)
このようにニューラルネットワークの出力計算は入力が与えられると上の計算を繰り返すことで出力を求めることができます。
出力はどれだけ正確か?誤差関数を導入する
私たちの目標は適切に重み$\bf{w}$を調整することで入力$\bf{x}$から得られる出力$\bf{y}$が正解$\bf{d}$になるべく近づけることです。
ではどのように正解とどれだけ近いかを判断するのでしょうか。「正解との近さ」を定量的に表すために導入されたものが誤差関数です。機械学習における「学習」とは、課題に対する誤差関数を最適化(最小化)することで出力と正解を近づけようとすることに他なりません。
誤差関数が具体的にどのようなものか例を挙げながら紹介します。
回帰問題
回帰問題では出力データが正解を再現するような関数を見つける問題です。
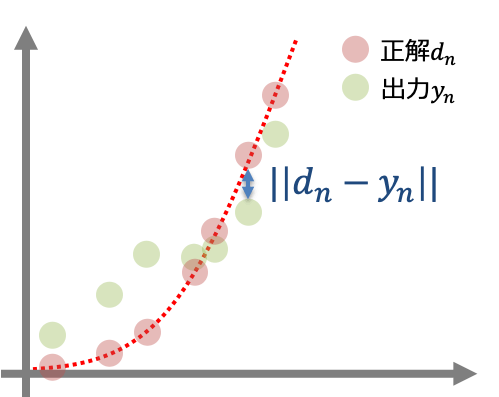
回帰問題において誤差関数$E(\bf{w})$は二乗誤差という表式が用いられます。
$$E(\bf{w}) = \frac{1}{2}\sum_n ||\bf{d}_n – \bf{y}(\bf{x}_n;\bf{w})||$$
シグマは各サンプルの二乗誤差の和を取る意味で用いています。また係数の1/2は誤差関数を微分した時に計算がしやすいというだけで特に深い意味はありません。
シグマの中をよく見ると二乗誤差とは出力と正解との距離を表すものであるということがわかります。二乗誤差は一般的に使われる誤差関数であり出力と正解との近さを直感的に表していると言えます。
分類(二値)問題
次に入力に対してAなのかBを分類する二値分類について考えます。二値分類では正解はA($d=0$)かB($d=1$)の二つの値しかとりません。二値分類問題では誤差関数は対数尤度というものが用いられます。
$$E(\bf{w}) = -\sum_n[d_n \log{y(\bf{x}_n;\bf{w})} + (1-d_n)\log{{1 – y(\bf{x}_n;\bf{w})}}]$$
なぜこのような複雑な関数が登場するかはこちらで解説します。
to be soon
以上のように入力から得られた出力を元に各課題に対する誤差関数を計算するところまでを学習しました。次は誤差関数を最適化するための計算手法である確率的勾配降下法について学習していきます。
まとめ
- ニューラルネットワークの出力計算は行列とベクトルを用いて計算できる
- 得られた出力と正解がどれだけ近いかは誤差関数によって評価する
- 誤差関数は課題によって異なり、学習とは誤差関数を最適化することを言う





コメント