量子シミュレーションのための量子回路の作り方

量子コンピュータの応用先の一つとして物理系のシミュレーション(何らかの基礎方程式に従う系の時間発展の追跡)が期待されています。

量子系のシミュレーションはサイズに対して計算コストが指数関数的増加するため、古典コンピュータによるシミュレーションでは限界があるとされています。そこで量子コンピュータで効率的にシミュレートしようと研究が進められています。

この記事では量子系のダイナミクスのシミュレーションを量子コンピュータでどのように実現するか、簡単な例で紹介します。

量子系のシミュレーションとは
1. 量子系のダイナミクスの一般論
2. tight-bindingモデルの例
トロッター分解
量子ゲートの考え方
IBM Quantum Challengeの問題にトライ
まとめ

量子系のシミュレーションとは

量子系のシミュレーションとは量子のダイナミクス(時間発展の様子)を把握することが目的です。まずは量子系のダイナミクスとは何かをおさらいしましょう。

量子系のダイナミクスの一般論

量子系はシュレーディンガー方程式と呼ばれる方程式に従って振る舞います。

シュレディンガー方程式とは、高校物理で学んだ物体の運動を記述する運動方程式と同じように、量子系の振舞いを記述する方程式です。

i\hbar\frac{\partial}{\partial t}|\psi(t)\rangle = \hat{H}|\psi(t)\rangle

量子系のダイナミクスとはシュレディンガー方程式を解である$|\psi\rangle$の時間発展の様子を掴むことが目的です。

ここでハミルトニアン$\hat{H}$が時間変化しない場合を考えると、シュレーディンガー方程式は単純な微分方程式とみなすことが出来るので、解が容易に求まります。(今回は簡単のためこちらのケースを考えていきます。)

|\psi(t)\rangle = e^{-i\bar{H}t/\hbar}|\psi(0)\rangle

この式は初期の量子状態$|\psi(0)\rangle$に対して何らかの(ユニタリ)演算$e^{-i\bar{H}t/\hbar}$が作用していると読み取れます。

つまり$e^{-i\bar{H}t/\hbar}$の部分を量子回路で表現出来ればこの量子系のダイナミクスを量子コンピュータでシミュレーション可能であることが分かります。

tight-bindingモデルの例

ハミルトニアン$\bar{H}$が抽象的だとイメージしずらいので、具体例としてtight-bindingモデルという物理のモデルを考えてみましょう。モデルの詳細は本記事の対象外なので、ここではただの数式とみなします。

\bar{H}_{tb}/\hbar=\sum_i\epsilon_iZ_i + J\sum_{< i,j >}(X_iX_j+Y_iY_j)

計算を簡単にするため$\epsilon_0, J=1$とすると、この量子系のダイナミクスは以下のように表すことが出来ます。

|\psi(t)\rangle = \exp[-it\sum_{< i,j >}(X_iX_j+Y_iY_j)]|\psi(0)\rangle

したがって$\exp[-it\sum_{< i,j >}(X_iX_j+Y_iY_j)]$を量子回路で表したいわけですが、このままの形式では1・2量子ビットゲートで表現できません。そこで登場するのがトロッター分解というテクニックです。

トロッター分解

トロッター分解とは数学的には以下の定義を持ちます。

トロッター分解の定義

$A, B$がエルミート行列のとき、以下が成り立つ。

\lim_{n\rightarrow\infin}(e^{iAt/n}e^{iBt/n})^n=e^{i(A+B)t}

これはごく短い時間幅$\Delta t=t/n$の間であれば、右辺で表現される量子回路は$A,B$の各項を表現する量子回路を並べた結果で近似できることを表しています。

トロッター分解をtight-bindingモデルの解に適用すると以下のように表すことが出来ます。式を見やすくするために2粒子系で考えます。

\begin{aligned} |\psi(t)\rangle &= \exp[-it(X_1X_2+Y_1Y_2)]|\psi(0)\rangle \\ &\sim \exp[-i\Delta tY_1Y_2] \exp[-i\Delta tX_1X_2]|\psi(0)\rangle \end{aligned}

以上のようにこのモデルのシミュレーション回路を作るには$\exp[-i\Delta tX_1X_2]$と$\exp[-i\Delta tY_1Y_2]$を量子回路で表現出来ればよいということが分かりました。

量子ゲートの考え方

それでは$\exp[-i\Delta tX_1X_2]$と$\exp[-i\Delta tY_1Y_2]$がどんな量子ゲートで表すことが出来るのかを考えていきます。

Zの場合

まずは最も単純な$\exp[-i\Delta t Z]$から考えてみましょう。

e^{-iZt}= \begin{pmatrix} e^{-it} & 0 \\ 0 & e^{it} \end{pmatrix}

これは$|0\rangle$と$|1\rangle$を固有状態に持ち、固有値はそれぞれ$e^{-it}$と$e^{it}$なので、$\exp[-i\Delta t Z]$とは以下の位相シフトを行うゲートと考えることが出来ます。

$|0\rangle$に作用する場合・・・$e^{-it}$
$|1\rangle$に作用する場合・・・$e^{it}$

このような振る舞いをする身近な量子ゲートを思い出してみると、Z回転ゲートがマッチすることが分かります。

R_z(\theta)= \begin{pmatrix} e^{-i\theta/2} & 0 \\ 0 & e^{i\theta/2} \end{pmatrix}

したがって指数がZゲートの場合、Z回転ゲートで表せることが分かります！

e^{-iZt} = R_Z(2t)

ZZの場合

では指数がZZの場合を考えてみましょう。同じように考えると次の位相シフトが考えられます。

$|00\rangle$または$|11\rangle$に作用する場合・・・$e^{-it}$
$|01\rangle$または$|10\rangle$に作用する場合・・・$e^{it}$

この条件は$|1\rangle$の状態の量子ビットが偶数か複数かと読み替えることが出来ます。そしてその判定はCNOTゲートを使うことで実現可能です。

1番目の量子ビットを制御、2番目の量子ビットを標的ビットとみなすと、CNOTを作用させたときの状態によって判定が可能です。

$|0\rangle$・・・$|1\rangle$の状態の量子ビットが偶数個
$|1\rangle$・・・$|1\rangle$の状態の量子ビットが奇数個

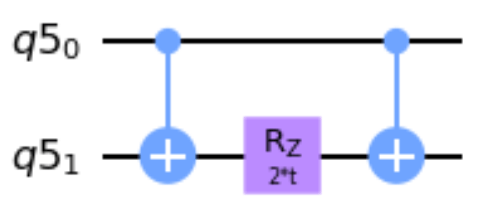
以上を踏まえると指数がZZの場合はCNOTとZ回転ゲートで表せることが分かりました。

XX・YYの場合

ZZが分かってしまえば、Z軸から見ていた世界をX・Y軸から見ればいいだけです。これを可能にするのがクリフォードゲートという量子ゲート群になります。

クリフォードゲートとはパウリゲートを他のパウリゲートにマッピングする量子ゲートのことで、アダマールゲートやSゲートが該当します。

HZH=X\\ SXS^{\dagger}=Y

つまりZ軸で見ていた世界はアダマールゲートで挟むとX軸から見る世界となり、X軸で見ていた世界はSゲートで挟むとY軸から見る世界となります。

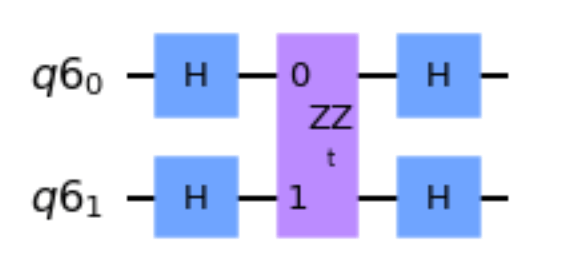
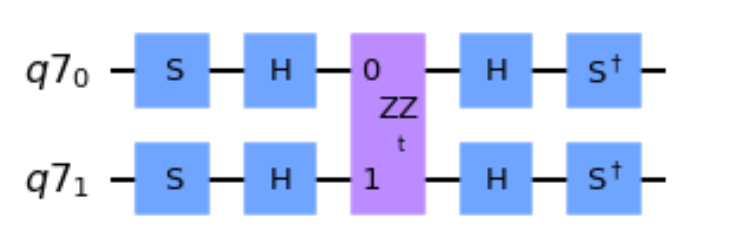
このように考えると、XX・YYは以下の量子回路で表すことが出来ることは納得がいくでしょう。

以上でtight-biindingモデルのダイナミクスをシミュレーションするための考え方は理解いただけたと思います。

IBM Quantum Challengeの問題にトライ

以上の内容はIBM Quantum Challenge 2022 Springの第1問で扱われています。ここではせっかくなので問題の一部にトライしてみましょう。

question 1a

$\exp[-i\Delta tX_iX_j]$を量子回路で表現せよという問題です。先ほどやりましたね。Qiskitで次のように書くことが出来ます。

XX_qr = QuantumRegister(2)
XX_qc = QuantumCircuit(XX_qr, name='XX')


XX_qc.h(0)
XX_qc.h(1)


XX_qc.append(ZZ, [0,1])


XX_qc.h(0)
XX_qc.h(1)


# Convert custom quantum circuit into a gate
XX = XX_qc.to_instruction()

XX_qc.draw('mpl')

ただしZZに関しては事前定義が必要です。

# Build a subcircuit for ZZ(t) from single- and two-qubit gates

ZZ_qr = QuantumRegister(2)
ZZ_qc = QuantumCircuit(ZZ_qr, name='ZZ')

ZZ_qc.cnot(0,1)
ZZ_qc.rz(2 * t, 1)
ZZ_qc.cnot(0,1)

# Convert custom quantum circuit into a gate
ZZ = ZZ_qc.to_instruction()

ZZ_qc.draw('mpl')

question 1b

$\exp[-i\Delta tY_iY_j]$を量子回路で表現せよという問題です。これも同様です。

YY_qr = QuantumRegister(2)
YY_qc = QuantumCircuit(YY_qr, name='YY')

YY_qc.s(0)
YY_qc.s(1)
YY_qc.h(0)
YY_qc.h(1)

YY_qc.append(ZZ, [0,1])

YY_qc.h(0)
YY_qc.h(1)
YY_qc.sdg(0)
YY_qc.sdg(1)

# Convert custom quantum circuit into a gate
YY = YY_qc.to_instruction()

YY_qc.draw('mpl')