量子機械学習アルゴリズムの1つである量子回路学習(Quantum Circuit Learning: 以下QCL)をQiskitを使って実装し、$y = \sin x$を学習させてみました。
はじめに
本記事はQuantum Native Dojo 5-2「Quantum Circuit Learning」を元に執筆しています。アルゴリズムの詳細はこちらをご覧ください。
教師データの準備
まずは教師データを準備します。$y = \sin x$にノイズを加えたものを教師データとして利用します。
# 現実のデータを用いる場合を想定しノイズを付加
mag_noise = 0.05
y_train = y_train + mag_noise * np.random.randn(num_x_train)
plt.plot(x_train, y_train, "o"); plt.show()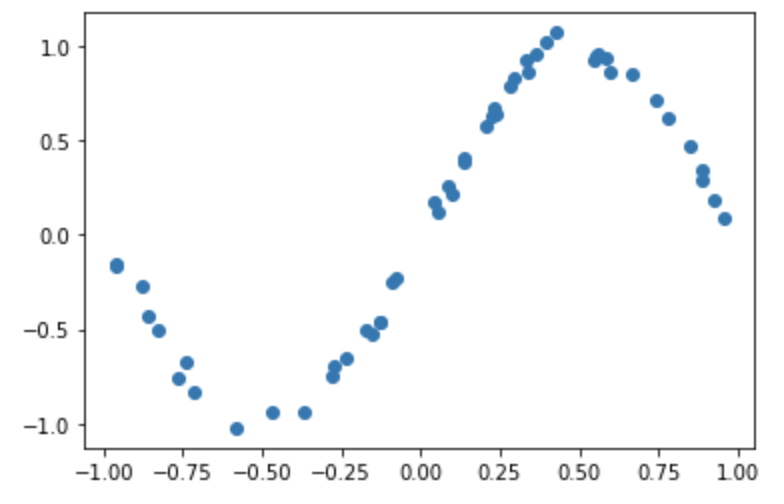
入力をエンコードする量子回路$U_{in}$を実装する
入力データ${x_i}$を量子状態へエンコードして入力状態$|\psi_{in}(\bm{x})\rangle$を生成するための量子回路$U_{in}$を実装します。
元論文に従い、$U_{in} = \prod_j R_j^Z(\arccos x^2) R_j^Y(\arcsin x)$と定義します。
def U_in(x):
U = QuantumCircuit(nqubit)
angle_y = np.arcsin(x)
angle_z = np.arccos(x**2)
for i in range(nqubit):
U.ry(angle_y, i)
U.rz(angle_z, i)
return Uパラメータ化量子回路$U(\theta)$を実装する
パラメータ化された量子回路$U(\theta)$を入力状態$|\psi_{in}(\bm{x})\rangle$に作用させることで出力状態を得ますが、このとき大切なのは$U(\theta)$によりモデルの表現力を高められるかということです。
つまり重ね合わせが生じて複雑な非線形関数を基底関数として登場させることが重要です。ここでは物理的な実装も比較的容易で現実的である横磁場イジングモデルの時間発展演算子を用います。
横磁場イジングモデルは下のハミルトニアンで与えられる物理系です。
$$\hat{H} = \sum_{i=1}^nZ_iZ_{i+1} + h\sum_{i=1}^nX_i$$
この系の時間発展を量子ゲートとして扱うので、$U(\theta) = e^{-i\hat{H}t}$となります。
# 横磁場イジングモデルのパラメーター
time_step = 0.77 # ランダムハミルトニアンによる時間発展の経過時間
M = 2 # トロッター分解の分割数
delta = time_step/M # 時間の刻み幅
h = 3 # 外部磁場
# 回転ゲートのパラメーター
param_list = ParameterVector('theta', c_depth*nqubit*3)def U_out():
qc = QuantumCircuit(nqubit)
for d in range(c_depth):
for s in range(M):
# トロッター分解の1回分、
for i in range(nqubit):
qc.cx(i,(i+1)%nqubit)
qc.rz(-2*delta,(i+1)%nqubit)
qc.cx(i,(i+1)%nqubit)
qc.rx(-2*delta*h, i)
# 回転ゲートを導入
for i in range(nqubit):
qc.rx(-2*param_list[3*(nqubit*d+i)], i)
qc.rz(-2*param_list[3*(nqubit*d+i)+1], i)
qc.rx(-2*param_list[3*(nqubit*d+i)+2], i)
return qcここで元記事であるQuantum Native Dojoでは横磁場イジングモデルのハミルトニアンの行列を求めて量子ゲート化するという手順を踏んでいますが、本記事ではより量子回路を利用してTrotter分解を利用して時間発展演算子を量子回路化しています。
Trotter分解を利用した時間発展演算子の量子ゲートへの実装についてわからない方はこちらをご覧ください。
モデルの出力を求める
モデルの出力を求めるために、今回は1番目の量子ビットの計算基底での期待値測定を行った結果を取得します。
def qcl_pred(x, param_dict):
qcl_cirq = U_in(x) + U_out()
qcl_cirq.assign_parameters(param_dict, inplace=True)
op = Z ^ I ^ I
psi = StateFn(qcl_cirq)
return 2 * get_expectation_val(psi, op)コスト関数の最適化
以上でモデルを構築する準備ができたので学習を開始します。今回コスト関数は教師データと出力との平均二乗誤差を用います。
def cost_func(theta_list):
param_dict = dict(zip(param_list.params, theta_list))
# num_x_train個のデータについて計算
y_pred = [qcl_pred(x, param_dict) for x in x_train]
# quadratic loss
L = ((y_pred - y_train)**2).mean()
return L学習にはscipy.optimize.minimizeを用います。適当な初期パラメータを与えた後にコスト関数を最適化するようなパラメータを求めます。今回は最適化手法に勾配計算を伴わないNelder-Mead法を用いています。
学習には私の環境で2時間近くかかってしまったので気長にお待ち下さい。
from scipy.optimize import minimize
result = minimize(cost_func, theta_init, method='Nelder-Mead')
theta_opt = result.x
print(theta_opt)結果
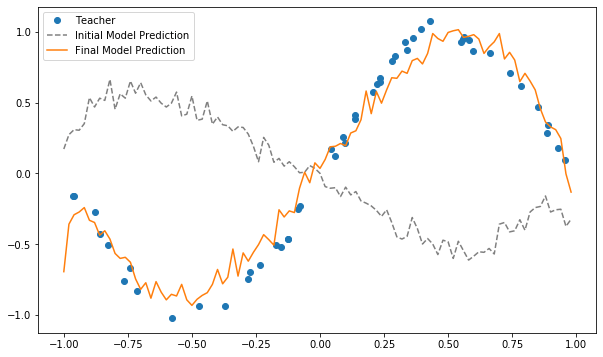
下が学習結果です。青の点が教師データ、オレンジの実線が学習モデルです。ひとまず概ねうまく学習できていることがわかります。
モデルのノイズが大きいのは出力状態の期待値を求めるときに1024回のshot測定を行った平均値として計算しているためです。
以上のようにQiskitを使って量子回路学習を実装することができました。
ソースコード
本記事に掲載したソースコードは抜粋した一部です。自分で動かしたい、すべてのコードを見たいという方はこちらのGitHubにソースコードを載せているので興味があったら覗いてください。








コメント