量子コンピュータで最適化問題を扱うためのQUBO変換

最適化問題は量子コンピュータの応用分野として注目されています。

最適化問題では問題を最適化関数にモデル化することで、最適化関数の最小値を取るようなパラメータが扱う問題のベストな方法となるようにします。

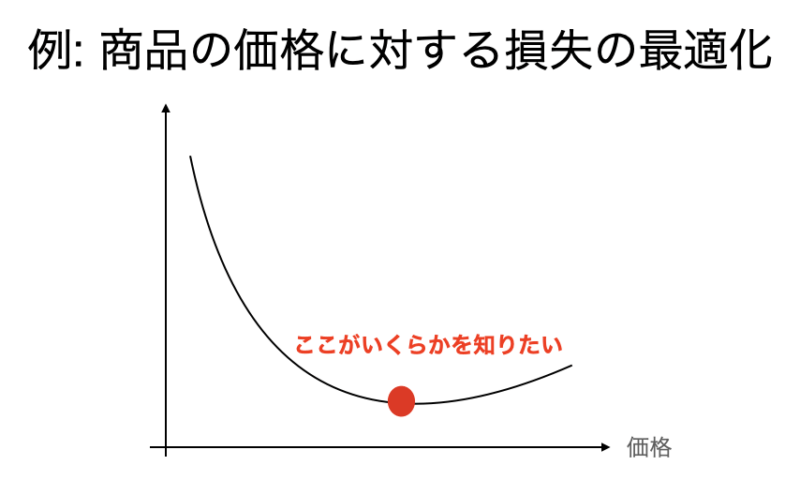
ではモデル化して定義された最適化関数はどのように量子コンピュータで扱えばよいのでしょうか。

実は最適化関数はQUBOという形式で表現される場合、量子コンピュータのイジングモデルと等価であることが数学的にわかっています。

この記事では量子コンピュータが最適化問題を具体的にどのように読み替えて計算するのかについて紹介します。

量子コンピュータの計算には量子ゲートが必要

まず量子コンピュータで計算を行うためには、量子ゲートの集まりからなる量子回路を組むことが必要です。

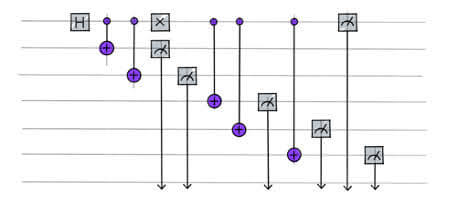
つまり最適化問題を量子コンピュータで扱うためには最適化関数が量子回路で表現できる必要があります。

量子系のエネルギー最小化問題とのアナロジー

最適化関数を量子回路へと読み替える必要があることはわかったところで、最適化問題から話は変わって量子化学や物性物理の問題へと目を向けてみます。

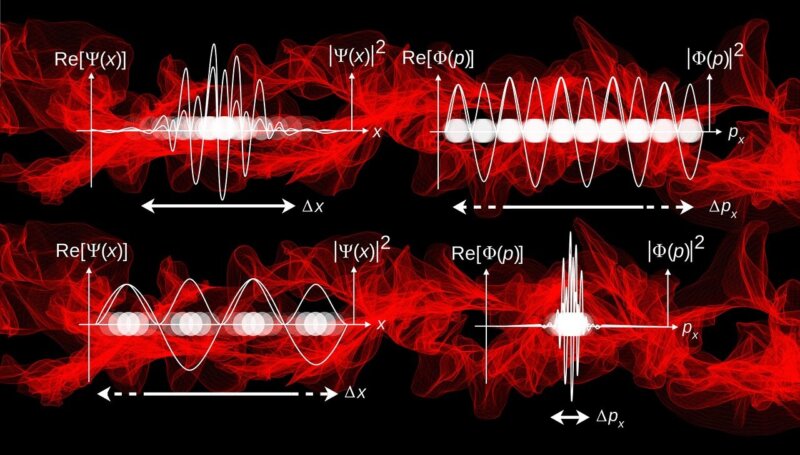
量子化学の分野では量子多体系の振る舞いが発現する物性が着眼点です。物性を知る上で最も基本的な情報となるのは量子系のエネルギー状態、特に最小値を取る基底状態のエネルギーです。

VQEなどは、量子系のエネルギー状態を表現する関数であるハミルトニアンの最小値を求めるためのアルゴリズムとして知られています。

ここで一歩立ち止まりましょう。

問題は違えどここで行っているのは関数の最適化であることは一緒です。であれば、一般の最適化問題も何らかの物理系と等価であれば同様に最適化できるのではないかと考えられます。

QUBO形式

視点を数学の最適化問題に戻します。

最適化問題でモデル化される関数は、多くがQUBO(Quadratic Unconstrained Binary Optimization: 2次制約なし2値最適化)の形式で表現できることが知られています。

$q_i, q_j$は0または1のいずれかをとる2値変数です。

C(\bm{q})=\sum_{i,j} C_{ij}q_iq_j

この関数の形は量子系の最も基本的なモデルであるイジングモデルのハミルトニアンと同じです。

H = \sum_{ij}J_{ij}Z_iZ_j

つまり、QUBO形式で表現される最適化関数はイジングモデルの量子系のエネルギー最小化問題と等価であり、量子コンピュータで最適化計算を行う事ができます。

イジングモデルのハミルトニアンへの変換

QUBOの2値変数は$x\in{0,1}$、一方イジングモデルの2値変数は$x\in{1,-1}$を想定しているのでこの差分をマッピングすれば完全に等価な問題となります。

イジングモデルでZゲートが使われていたのはZゲートの表現行列の固有値が$\pm1$だからです。なので同じように固有値が$0,1$であるようなゲートに置き換えれば良いことになります。

一般的には$(I-Z)/2$の演算子が使われます。

\frac{I-Z}{2}|0\rangle = 0|0\rangle \\
 \frac{I-Z}{2}|1\rangle = 1|1\rangle

これで最適化関数が定義できたら機械的に量子回路を組み立てることができるようになりました

例題：Max-Cut問題

Max-Cut問題を例に確認しましょう。

Max-Cut問題

重み付きグラフのノードを2つのグループに分けるとき、グループをまたぐエッジの重みの総和を最大化する問題。

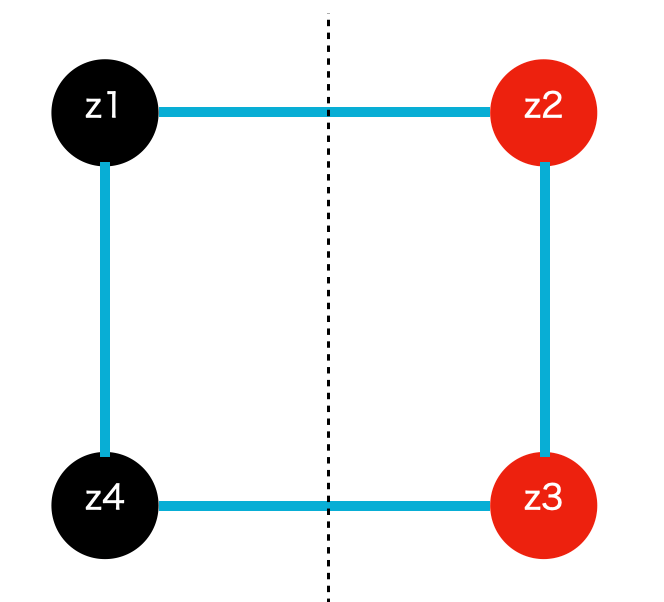
最適化関数は同じグループどうしの場合は寄与せず、異なるグループの場合のみ重みをカウントすればよいので下のような形式でモデル化することができます。

C(z)=-\frac{1}{2}\sum_{i,j} C_{ij}(1-z_iz_j)

ここまでの話の内容を適用すると、この最適化関数は下のハミルトニアンを持つイジングモデルのエネルギー最小問題とみなすことができます。(簡単のため$C_{ij}=1$とします。)

本来はQUBOに変換して考えるのですが、たまたまモデルの2値変数が$\pm1$であるため、変数をそのままZゲートに置き換えるだけで済みそうです。

\begin{aligned}
H&=-\frac{1}{2}\sum_{i,j}(1-Z_iZ_j)  \\
&=\frac{1}{2}(Z_1Z_2+Z_2Z_3+Z_3Z_4+Z_4Z_1)-2 
\end{aligned}

ハミルトニアンが得られたらエネルギー最小化問題として解けば良いのでVQEやQAOAといったアルゴリズムが適用可能な状態となります。

まとめ

この記事では量子コンピュータで一般の最適化問題を量子系のエネルギー最小化問題とみなすことで計算が可能となる理由について紹介しました。

本記事の考え方はQiskitなどのライブラリの裏側で実際に行われている処理です。ライブラリではパラメータを渡すとハミルトニアンを返してくれますが、裏では同じ計算をしています。