
決定木モデルは他のモデルよりも解釈がしやすく可視化が可能という点で優れたモデルです。決定木はデータを何かしたの条件で繰り返し場合分けを行うことで分類する手法です。
例:会社員の通勤手段の分類を考える
決定木で会社員の通勤手段を分類してみましょう。例えば通勤に10km以上かかるかという条件で場合分け、次に…と場合分けを繰り返して分類することができます。
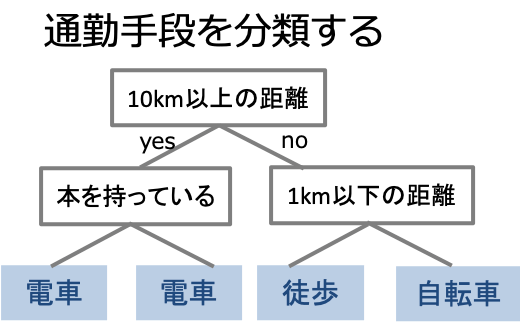
この時場合分けは情報利得(Information gain)が最大となるように行われます。理想的な分割とは分割されたデータが全て同じラベルとなる状態です。つまり情報利得とは分割したデータの同質性であると考えることができます。
では実際にscikit-learnを使って決定木を実装してみましょう。ここではscikit-learnに組み込まれているIrisデータセットを使って実装していきます。
Irisデータセットとは?
Irisデータセットとは4つの特徴量(がく・花弁のそれぞれ幅と長さ)から3種類のIris(アヤメ)を分類したものです。このデータセットは機械学習で広く使われている有名なデータセットです。

- 4つの特徴量(がく・花弁の幅、長さ)
- 3種類のラベル(Setosa, Versicolor, Virginica)
- サンプル数は150個(それぞれ50個ずつ)
scikit-learnで決定木を実装してみよう
データセットの理解ができたので実際に決定木による分類を行いましょう。
まずはIrisデータセットを読み込んで学習モデルを構築するための訓練データと予測を行うためのテストデータに分割しましょう。
#Irisデータセットを読み込む from sklearn import datasets from sklearn.model_selection import train_test_split iris = datasets.load_iris() X = iris.data y = iris.target #訓練データとテストデータに分割 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, stratify=y, random_state=1)
決定木モデルのインスタンスを作成して訓練データを学習させましょう。
#決定木分類器をインポート from sklearn.tree import DecisionTreeClassifier #インスタンスを作成 dtc = DecisionTreeClassifier() #学習を行う dtc.fit(X_train, y_train)
Out:
DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=None,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False, random_state=None,
splitter='best')In :
#正解率を確認 from sklearn.metrics import accuracy_score y_pred = dtc.predict(X_test) accuracy_score(y_test, y_pred)
Out:
#正解率 0.9666666666666667
この結果から今回作成した決定木モデルが良い分類器として機能していることがわかります。
それでは決定木の優れた長所である結果の可視化を行いましょう。
#pydotを使って決定木を可視化 from sklearn import tree from sklearn.externals.six import StringIO import pydotplus as pdp from IPython.display import Image dot_iris = StringIO() tree.export_graphviz(dtc, out_file=dot_iris, feature_names=iris.feature_names) graph= pdp.graph_from_dot_data(dot_iris.getvalue()) Image(graph.create_png())
Out:
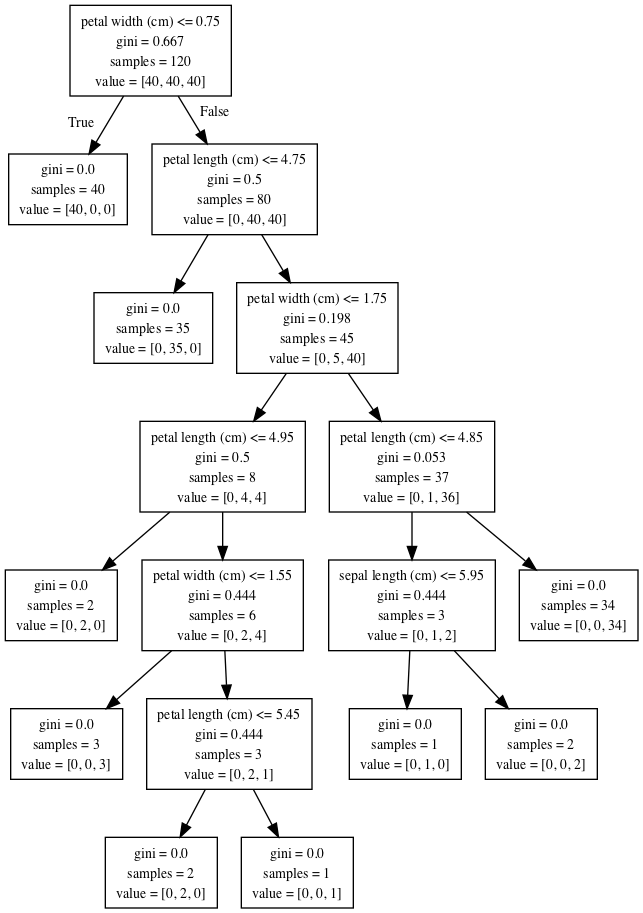
今回学習に使われた訓練データはサンプル数が120個で3種類のアヤメが均等に40個ずつ分布するように生成しました。(In[1]のtrain_test_splitの部分)
結果を見ると一番最初の場合分けはpetal widthが2.7cm以下かどうかとなっています。花弁の幅が2.7cm以下のサンプルは1つ目のラベル(value=[40,0,0])のSetosaに分類されます。偽の場合は残りの2つ(value=[0,40,40])であるVersicolorとVirginicaのみが入っています。
場合分けは情報利得が最大となるような条件で行われ、最終的に分割したデータのラベルが同じになった時点で分割を終了しています。
Gini不純度とは?
ここで一つ気になるのは結果の各ノードに記されているginiという量だと思います。実はこれが初めに書いた不純度$I$を表すジニ不純度という量です。ジニ不純度は二分決定木の場合、誤分類の割合を$p$とおくと
$I_gini(D) = p(1-p)$
で定義されます。先ほどの決定木はこの時に不純度を最適化するようにデータを分割していました。
ちなみに不純度の指標にはもう一つ代表的なものとして情報エントロピーがあります。
$I_entropy(D) = -plog_2(p)-(1-p)log_2(1-p)$
これらの指標はスケールを合わせると誤分類の割合pに対して下の図のようなグラフになります。つまりデータを分類した時に正解率がある程度高い($p$が小さい)時はエントロピーの方がジニ不純度よりも高い得点を与えていることがわかります。この違いが分割に影響を与えうるのです。
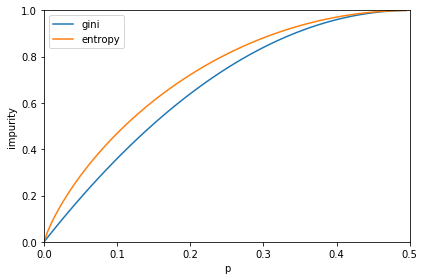
それではエントロピーを使った決定木でも学習させてみましょう。
dtc = DecisionTreeClassifier(criterion='entropy') dtc.fit(X_train, y_train)
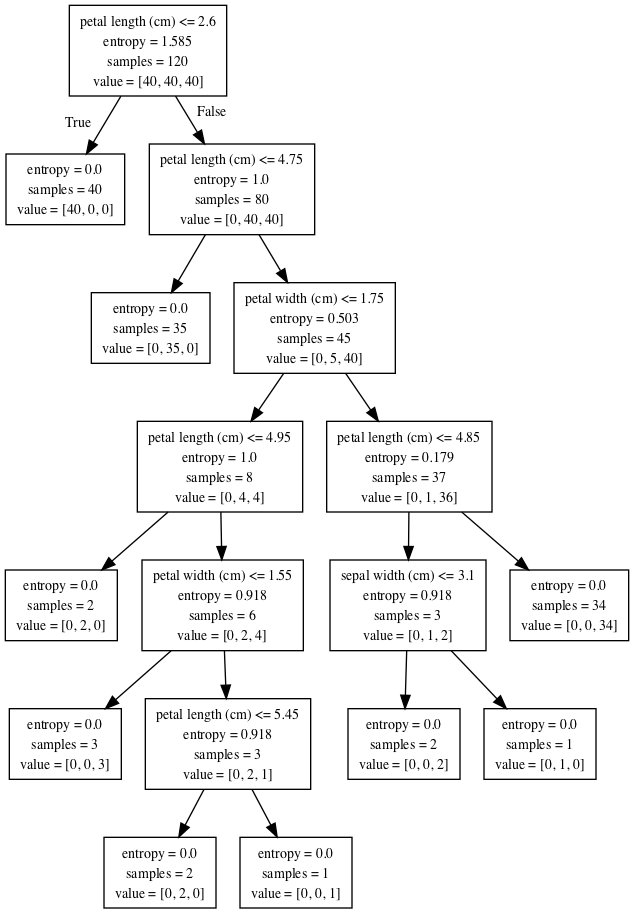
ほとんど同じような結果が出てきましたが、一部分割に差が見られます。実際のモデル構築においては交差検証などでモデルをチューニングしてどちらの不純度を用いるのがベストかを決定します。
まとめ
決定木は意味解釈性が高いことから相手に学習結果を相手に説明する時には非常に有効です。精度がそれほど求められない場面であれば精度を犠牲にしてでも決定木を採用することもあるそうです。






コメント