バギングって何ですか？目で見てわかるメリットとは

機械学習で決定木の勉強をしていると知らない言葉がたくさん出てきて困りますよね。

ランダムフォレスト、バギング、ブースティング…など初めて聞く言葉ばっかりで心が折れてしまいそうです。知らない単語に圧倒されて大筋を見誤らないためにそれぞれの単語の意味と立ち位置を整理していきます。

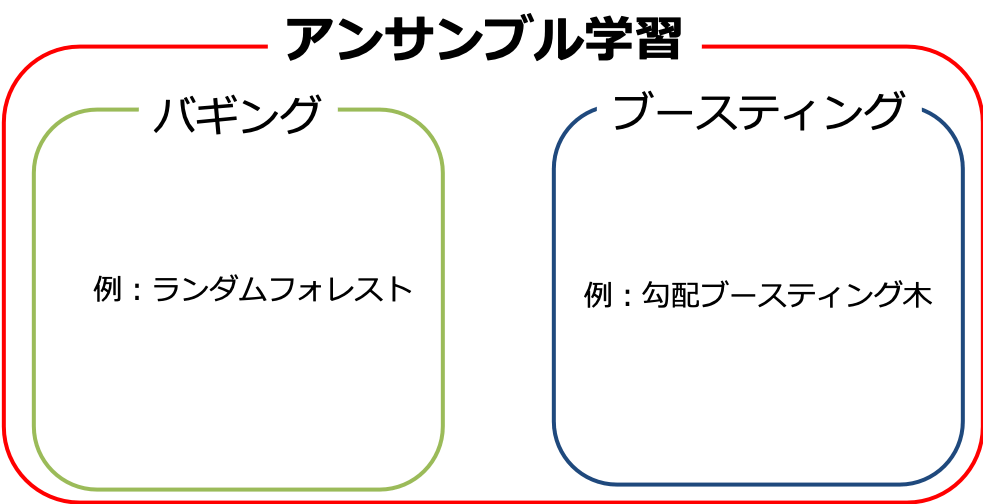
まずバギングやブースティングといった単語はアンサンブル学習という手法で登場します。

アンサンブル学習とは予測性能が高くない学習モデル（弱学習器）を組み合わせることで性能を向上させる手法です。

経験的に予測性能が向上することが知られていて、アンサンブル学習の具体的なアルゴリズムがバギングやブートストラップです。

今回は2つのうちバギングの手法について理解することを目標にします。

バギングとは

バギング（Bootstrap AGGregatING）とはデータセットから重複を許してランダムに抽出した訓練データを複数用意し、それぞれ独立にモデルを学習させて出力を各モデルの平均や多数決をにより決定する手法です。

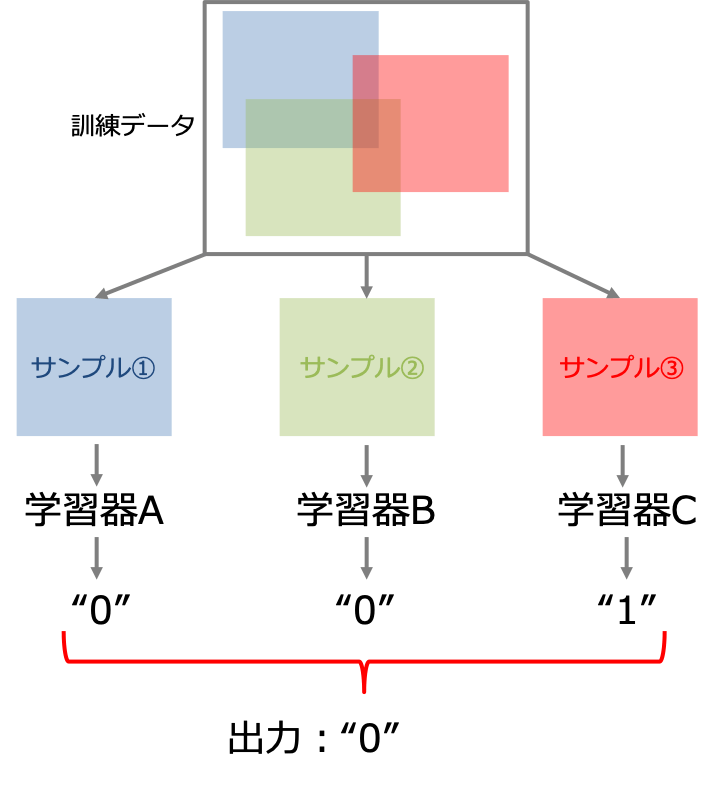
バギングによって予測精度が不安定なモデルの性能を向上させて過学習を抑えることができます。これをpythonで確かめてみましょう。今回はWineデータセットを用いて実装していきます。

Wineデータセットを理解する

まずはWineデータセットがどんなデータなのかを理解しましょう。

Wineデータセットは13個の科学的特徴から3種類のラベルを分類するためのデータセットです。

バギングをpythonで実装する

それでは実装していきます。

学習に必要なデータを用意

まずはWineデータセットをインポートしましょう。Wineデータセットはscikit-learnに元々組み込まれているためload_wineで呼び出します。

また今回は予測に使う特徴量として’alcohol’と’od280/od315_of_diluted_wines’を使うことにします。（アルコールと希釈ワイン中のタンパク質の割合？）

#pandasをインポート
import pandas as pd

#wineデータセットのインポート
from sklearn import datasets
wine = datasets.load_wine()

#特徴量とラベルを一つのデータフレームに結合(以下で特定のラベルを抽出するため)
X = pd.DataFrame(wine.data, columns=wine.feature_names)
y = pd.DataFrame(wine.target, columns=['label'])
df_wine = pd.concat([X, y], axis=1)

#クラス1とクラス2のワインを選択
df_wine = df_wine[df_wine['label'] != 0]
#特徴量は'od280/od315_of_diluted_wines',とalcohol'の2つを使用
X = df_wine[['od280/od315_of_diluted_wines', 'alcohol']].values
y = df_wine['label'].values

ここでワインのラベルは0,1,2の数値型であるため符号化してカテゴリー変数として扱います。

#クラスラベルを符号化
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
y = le.fit_transform(y)

#データセットを訓練データとテストデータに分割する
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, stratify=y, random_state=1

決定木を使ったバギングのモデルを構築

決定木モデルを使ってバギングのモデルを構築します。

#決定木モデルを用いたバギングのインスタンスを生成
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier

tree = DecisionTreeClassifier(criterion='entropy', max_depth=None, random_state=1)
bagging = BaggingClassifier(base_estimator=tree,
                                            n_estimators=300,
                                            max_samples=1.0,
                                            max_features=1.0,
                                            bootstrap=True,
                                            bootstrap_features=False,
                                            n_jobs=1,
                                            random_state=1)

ラベルの予測

作ったモデルを使ってデータを予測します。まずは決定木モデル単体の予測の正解率を計算します。

from sklearn.metrics import accuracy_score
#モデルを学習させる
tree = tree.fit(X_train, y_train)

#訓練データとテストデータにおける予測の正解率を計算
y_train_pred = tree.predict(X_train)
y_test_pred = tree.predict(X_test)
score_train = accuracy_score(y_train, y_train_pred)
score_test = accuracy_score(y_test, y_test_pred)

#訓練データの正解率/テストデータの正解率
print('accueacy score of decision tree : %.3f/%.3f' % (score_train, score_test))

Out:

accueacy score of decision tree : 1.000/0.833

この出力は学習モデルが訓練データに対しては100%の正解率（完璧に予測できている）で、テストデータに対しては83.3%の正解率となっていて訓練データに過剰に適合した過学習となっていることがわかります。

次にバギングモデルを使って同じように予測を行います。

#モデルを学習させる
bagging = bagging.fit(X_train, y_train)

#訓練データとテストデータにおける予測の正解率を計算
y_train_pred = bagging.predict(X_train)
y_test_pred = bagging.predict(X_test)
score_train = accuracy_score(y_train, y_train_pred)
score_test = accuracy_score(y_test, y_test_pred)

#訓練データの正解率/テストデータの正解率
print('accueacy score of decision tree : %.3f/%.3f' % (score_train, score_test))

Out:

accueacy score of decision tree : 1.000/0.917

バギングモデルを使うことで決定木単体の場合と比べてテストデータに対する予測精度が向上していることがわかり、過学習が抑えられていることを確認できました。

結果の可視化

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

#プロット範囲を決定
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, 0.1), np.arange(x2_min, x2_max, 0.1))

#プロットを描く枠を用意
f, ax = plt.subplots(nrows=1, ncols=2)

#それぞれのモデルの結果を描く
for idx, clf, tt in zip([0, 1], [tree, bagging], ['Decision tree', 'Bagging']):
    #モデルの学習と予測
    clf.fit(X_train, y_train)
    Z = clf.predict(np.array([xx1.ravel(), xx2.ravel()]).T) #ravel()は多次元のリストを1次元に変換
    Z = Z.reshape(xx1.shape)
    #分類境界を描く
    ax[idx].contourf(xx1, xx2, Z, alpha=0.3)
    #各ラベルのサンプルを描く
    ax[idx].scatter(x=X_train[y_train==0, 0], y=X_train[y_train==0, 1], c='blue', marker='^')
    ax[idx].scatter(x=X_train[y_train==1, 0], y=X_train[y_train==1, 1], c='green', marker='o')
    #タイトル
    ax[idx].set_title(tt)

#軸ラベル
ax[0].set_ylabel('od280/od315_of_diluted_wines', fontsize=12)
ax[0].set_xlabel('alcohol', fontsize=12)

plt.tight_layout()
plt.show()

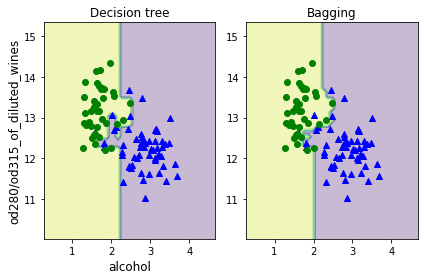
プロットを見てもバギングモデルの方がモデルの複雑性（バリアンス）が抑えられていることがわかります。

ただしバギングはバイアスを抑えることに関して効力を持ちません。そもそもモデルが単純すぎて予測性能が足りないという場合には有効でないという点に注意してください。

まとめ