量子アルゴリズムとしてよく登場するグローバーのアルゴリズムをQiskitを使ってゼロから実装する方法を紹介します。
グローバーのアルゴリズムの概要
グローバーのアルゴリズムとは$N$個の要素の中から特定の要素を探し出すアルゴリズムです。$N$枚の宝くじの中から当たりの1等を探しだすイメージです。

当たりを見つけるには、普通は平均$N/2$回あたりかはずれかを確認することが必要ですが、グローバーのアルゴリズムでは$\sqrt{N}$回の確認で済むという2次の量子加速をもつアルゴリズムです。
グローバーのアルゴリズムは他のアルゴリズムの基礎ともなる大切な考え方です。詳しい内容はこちらに書かれているので併せてご覧ください。
アルゴリズムのステップ
グローバーのアルゴリズムは以下のステップから構成されています。
- 【初期状態の準備】全ての量子ビットにアダマール変換を作用させる
- 【振幅増幅】以下の変換を$\Omicron (\sqrt(N))$回繰り返す
- オラクルに問い合わせる
- 拡散変換を作用させる
- 【結果の取得】得られた状態を測定する
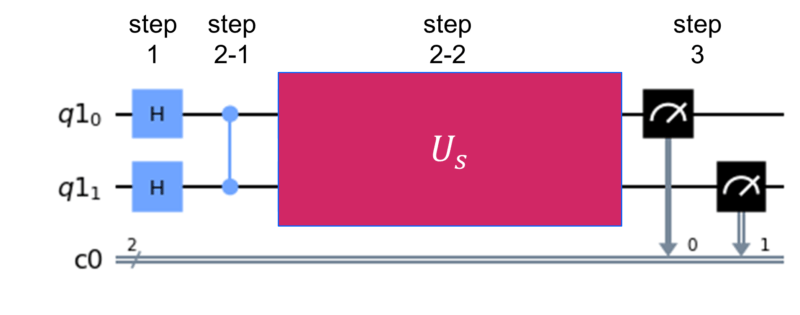
各ステップを量子回路に翻訳していくと下のような回路になります。
量子回路の実装と共に、それぞれのステップの意味についても以降で紹介します。
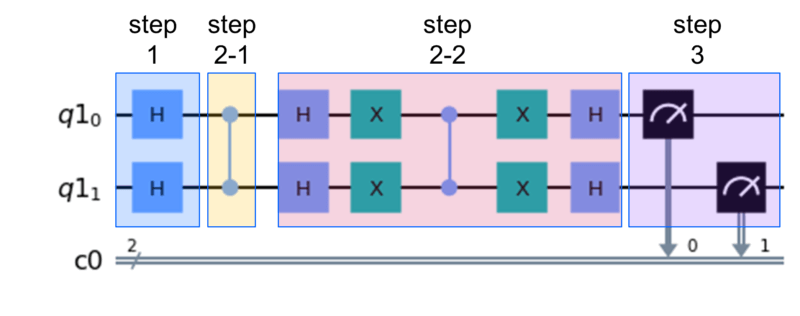
なお、簡単のため2量子ビット(宝くじが$2^2$枚)において、1等が$|11\rangle$の場合を考えることとします。
1.初期状態の準備
まずは量子計算のメリットを活かすための初期状態$|s\rangle$を準備します。
量子の重ね合わせを作り出すことで、$N$枚の宝くじから1枚選択したという$N$通りの状態を一度に扱えるようにします。
|0\rangle \rightarrow |s\rangle=\frac{1}{\sqrt{N}}(|00\rangle+|01\rangle+|10\rangle+|11\rangle)左から0番目、1番目のくじを選択した状態、一番右が$N$番目のくじを選択した状態と、考えられる4枚の全てのくじを引いた状態を持つ重ね合わせ状態を作り出します。
重ね合わせを作り出す操作はアダマールゲートにより実現出来ます。したがってStep1ではアダマールゲートを全ての量子ビットに適用します。
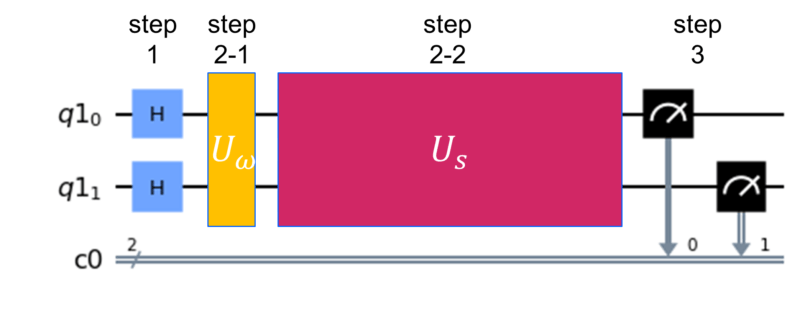
ここで、以降のステップを視覚的に理解するために今の状態を幾何学的に表現してみます。
1等を選択した正解の状態(今は$|11\rangle$)を$|w\rangle$、それに直交する不正解の状態$|s’\rangle$とおきます。つまり以下のような状態です。
|s\rangle =\sqrt\frac{N-1}{N}|s'\rangle + \frac{1}{\sqrt{N}}|w\rangleこの状態を$|w\rangle$と$|s’\rangle$で張られる2次元平面上を考えると下のように表現できます。ベクトルと思えば自然な表現です。
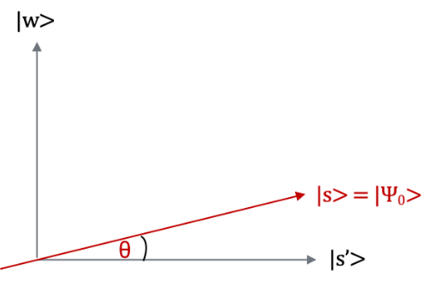
ここで縦軸は正解の状態$|w\rangle$が得られる確率が1、横軸は0であることを表しています。つまり以降のステップで行うべき操作は赤線を縦軸に近づけることになります。
2. 振幅増幅
重ね合わせの状態を準備したら、ステップ3で量子状態の観測を行った際に正解の状態$|w\rangle$が取得できるように$|w\rangle$の確率振幅を増幅する操作を行います。
2-1. オラクルに問い合わせる
まずはオラクルへの問い合わせという操作を通して正解の状態$|w\rangle$にマーキングを行います。
オラクルとは日本語で「神託」という意味を持つ言葉です。
神様に質問をすると答えが返ってくる様子に例えて、入力に対してそれが正解か不正解かの結果を返す仕組み(中身がブラックボックスな関数)をオラクルと呼びます。
グローバーのアルゴリズムにおけるオラクル$U_\omega$は、入力が正解の状態の場合は振幅の符号を反転させ、それ以外の場合は何もしないという結果を返すように構築されます。
つまり正解の状態$|w\rangle$には振幅の符号が反転というマーキングを行っていることになります。
U_\omega|s\rangle =\sqrt\frac{N-1}{N}|s'\rangle - \frac{1}{\sqrt{N}}|w\rangleこのオラクルの操作は、先ほどの幾何学表現において$|s’\rangle$に関する鏡映操作と考えることが出来ます。
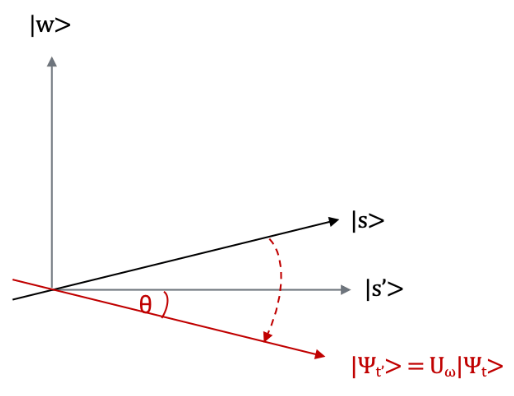
ではオラクルをQiskitで実装してみましょう。今回は入力が$|11\rangle$の場合に符号反転させる操作を考えればよいことになります。これは制御Zゲートにより実現できることが分かります。
制御Zゲートによりコントロールビットが1の状態のときにターゲットビットにZゲートが作用しますが、ターゲットビットが0の場合は影響がないため、11の状態の場合のみ位相反転を実現することが出来ます。
| コントロールビット | ターゲットビット | 出力 |
|---|---|---|
| $|0\rangle$ | $|0\rangle$ | $|00\rangle$ |
| $|0\rangle$ | $|1\rangle$ | $|01\rangle$ |
| $|1\rangle$ | $|0\rangle$ | $|10\rangle$ |
| $|1\rangle$ | $|1\rangle$ | -$|11\rangle$ |
2-2. 拡散変換を作用させる
続いて2-1で得られた状態を$|w\rangle$に近づけるために、$|s\rangle$に関する鏡映操作である拡散変換$U_s$を作用させます。
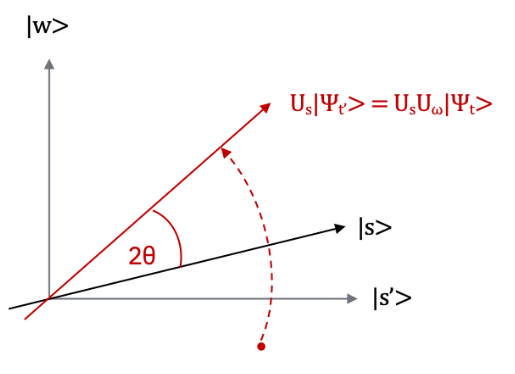
この操作により得られる状態$U_sU_{\omega}|\Psi_t\rangle$はステップ2はじめの状態$|s\rangle$よりも正解$|w\rangle$の確率振幅が大きいことがわかります。
ではどのようにこの鏡映操作を実現するかを考えていきましょう。説明の都合上$|s\rangle$に直行するベクトルを$|l\rangle$とおきます。
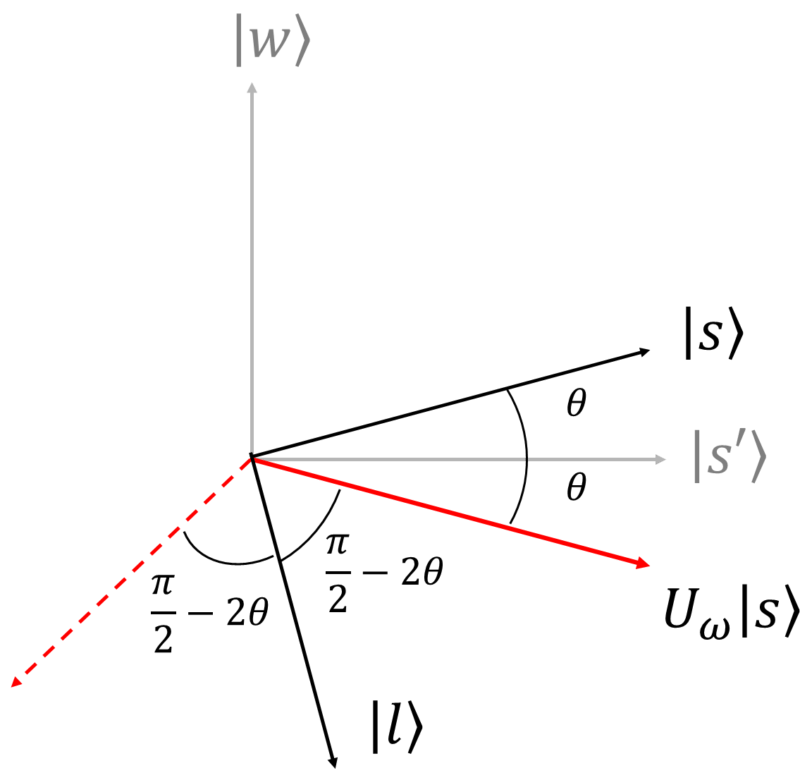
先ほどは$|s’\rangle$に関しての鏡映操作は扱えるようになったのでこれをうまく活用しましましょう。
今回は鏡映軸が$|s’\rangle$から$|s\rangle$に変わっているので、軸の変換を行えばよいのですが、$|s’\rangle$が少々複雑なので、一旦鏡映軸を$|s\rangle$ではなく$|l\rangle$で考えてみます。
上の図を見ると、$|l\rangle$に関する鏡映操作は鏡映軸を一旦$|s’\rangle$に変換してオラクルの操作を行えばよいとわかります。このとき、$|l\rangle\rightarrow|s’\rangle$の軸変換は$|s\rangle\rightarrow|w\rangle$と同義です。
従って$|s\rangle\rightarrow|w\rangle$の軸変換の後にオラクル$U_{\omega}$を作用させると$|l\rangle$に関する鏡映操作を実現できることになります。(赤点線)
このとき、赤点線は180度折り返すと$U_{\omega}|s\rangle$を$|s\rangle$に対して鏡映操作$U_s$を行った結果であることが確認できます。
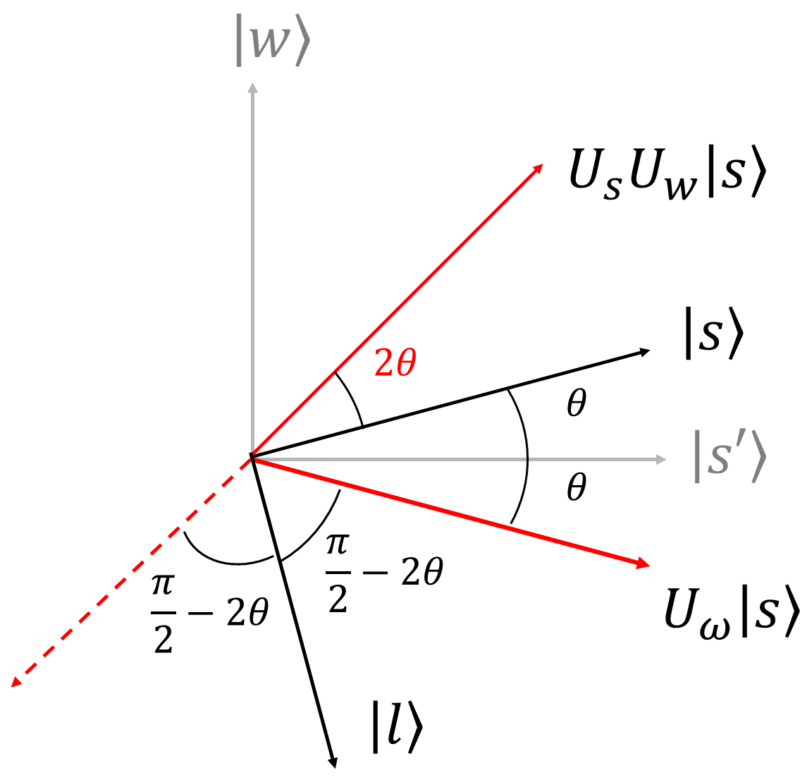
上図において180度折り返すというのは全体の振幅の符号を反転させる(グローバル位相を$\pi$ずらす)ことと同義です。
それでは鏡映操作の組み立て方が分かったところで、量子回路をQiskitで実装しましょう。
- 軸変換$|s\rangle\rightarrow|w\rangle$を行う。
- 鏡映操作$U_{\omega}$を適用する。
- グローバル位相を$\pi$シフトする。
- 1の軸変換の逆演算を行い元に戻す。
1に関しては今回$|w\rangle=|11\rangle$なので、$|s\rangle\rightarrow|11\rangle$の操作を行えばよいことになります。これはアダマールゲートとXゲートで容易に実現可能です。
3は量子操作においてグローバル位相は無視できる(測定から求まる状態の確率は振幅の2乗であるため、全体の符号が正だろうが負だろうが関係ない)ので、量子回路の操作として陽には表れません。
以上をまとめるとこのような量子回路により拡散変換を実現できます。
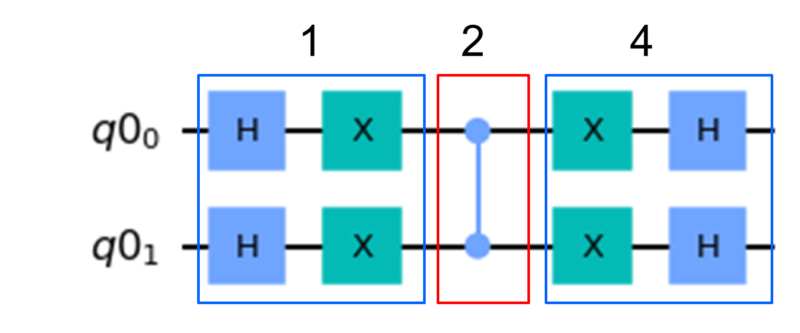
得られた状態を測定する
最後に計算結果を取得するために量子状態を測定します。以上をまとめると、グローバーのアルゴリズムは以下の量子回路で実装できることが分かります。
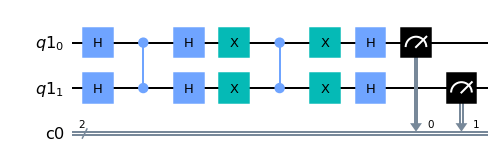
コードの全体はこちらです。
#initialization
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
# importing Qiskit
from qiskit import IBMQ, BasicAer
from qiskit.providers.ibmq import least_busy
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, execute
def phase_oracle(circuit, register):
circuit.cz(register[0], register[1])
def inversion_about_average(circuit, register):
"""Apply inversion about the average step of Grover's algorithm."""
circuit.h(register)
circuit.x(register)
circuit.cz(register[0], register[1])
circuit.x(register)
circuit.h(register)
qr = QuantumRegister(2)
cr = ClassicalRegister(2)
groverCircuit = QuantumCircuit(qr,cr)
groverCircuit.h(qr) // step1
phase_oracle(groverCircuit, qr) // step2-1
inversion_about_average(groverCircuit, qr) step2-2
groverCircuit.measure(qr,cr) // step3
groverCircuit.draw(output="mpl")シミュレーターで実行してみると、確かに期待していた状態$|w\rangle=|11\rangle$を確率1で取り出すことが出来ています。

まとめ
この記事ではグローバーのアルゴリズムをQiskitで実装する方法について紹介しました。
特に拡散変換については量子回路の組み方の考え方の部分が曖昧のままになってしまっている方もいると思うので、理解の助けになれば幸いです。
より詳しく学びたいという方はこちらがおすすめですので、興味があればぜひ手に取ってみてください。
- (初級者向け)今度こそわかる量子コンピュータ
- (中級者向け)量子コンピューティング~基本アルゴリズムから量子機械学習まで~









コメント