Natural gradient(自然勾配)とは、普通の勾配(Vanilla gradient)の欠点である「モデルの特性の考慮」を取り込んだ概念です。
機械学習の最適化計算で最も基本的な手法である最急降下法は下記の式に従ってパラメータの更新を行いますが、必ずしもベストな選択とは言えません。
\bm\theta_{n+1} = \bm\theta_n - \eta \nabla f(\bm\theta_n)一般的に自然勾配は普通の勾配よりも最適化の性能が良いとされています。この記事では自然勾配について、普通の勾配との違いを感覚的に理解し、Qiskitでの実装方法を紹介します。
普通の勾配の問題点
そもそも普通の勾配がどういう場合に問題なのかQiskit Textbookの図を引用して考えていきます。
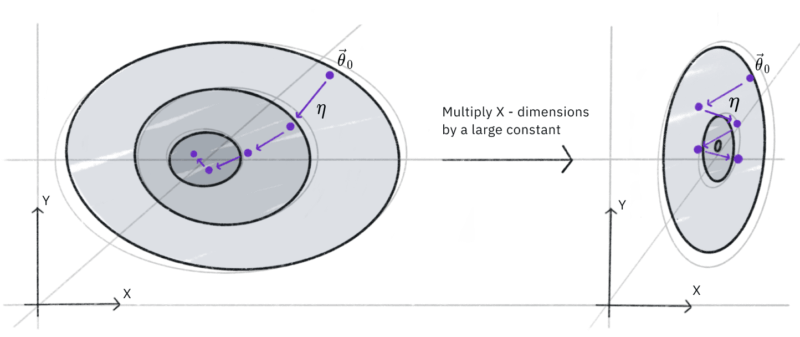
この図はパラメータ$\theta=(x, y)$に対するコスト関数の等値線図です(円の中央ほど値が小さい)。学習によってパラメータが最小値に近づくように更新されている様子を指しています。
普通の勾配を用いた最急降下法では、コスト関数が左の図のような場合スムーズに収束していますが、右の図の場合は最小値を行ったり来たりして効率的に収束していないことがわかります。
つまり難しいことを抜きにすると、コスト関数の形状によっては最急降下法ではスムーズに収束しないことがイメージできると思います。
自然勾配の特徴
最急降下法の欠点は冒頭で述べたようにコスト関数の形状がパラメータ更新に考慮されていないことです。
\bm\theta_{n+1} = \bm\theta_n - \eta \nabla f(\bm\theta_n)通常の勾配は学習率$\eta$がパラメータによらず一定であるために、このモデルのパラメータに対する感度を考慮出来ないことが非効率な学習を引き起こしているのです。
一方自然勾配では学習率がモデルに依存して変化するように設計されていているため、より高速な収束が可能となっています。
\bm\theta_{n+1} = \bm\theta_n - \eta g^{-1}(\bm\theta) \nabla f(\bm\theta_n)自然勾配の正体
ここで自然勾配の正体は曲がった空間における最急降下法であることを確認してみましょう。
始めに、最急降下法はユークリッド空間における世界を表現しています。ユークリッド空間では2点間の距離は内積で表すことが出来ました。(高校数学のベクトルを思い出してください)
||\bm\theta|| = \sum_{ij} \theta_i \theta_jではユークリッド空間でない曲がった空間を考えてみましょう。
曲がった空間での2点間の距離は、ユークリッド空間からの座標変換の影響を受けて以下のように表すことが出来るとしましょう。
||\bm\theta|| = \sum_{ij} g_{ij} \theta_i \theta_jこの曲がった空間において最適化計算を行うために、コスト関数の変化が最大となる方向を探します。
パラメータを適当な方向$\bm a$に変化させるとき、コスト関数の変化は以下のように表せます。
\Delta f = \eta \frac{\partial f}{\partial \bm \theta}\cdot\bm a$\bm a$はどの方向に対しても一定の大きさである必要があるため、この制約を満たしながら上記の変化が最大となる方向$\bm a$を探します。Lagrangeの未定乗数法を使うと
\delta(\frac{\partial f}{\partial \bm \theta}\cdot\bm a - \sum_{ij}\frac{\eta}{2}a_ia_j) = 0 \\
\therefore \bm a \propto g^{-1}\frac{\partial f}{\partial \bm \theta}したがって最急降下は$\bm a$と反対方向であればいいので、最終的な結果は以下のようになり、曲がった空間において最急降下と同じ考えをしていることが分かります。
\bm \theta_{n+1} = \bm \theta_{n} - \eta g^{-1}\frac{\partial f}{\partial \bm \theta}Qiskitで実装してみる
それでは自然勾配をQiskitを使って実装しましょう。自然勾配はNaturalGradientクラスを利用することで簡単に求めることができます。
from qiskit.opflow import NaturalGradient
ng = NaturalGradient().convert(expectation)
ng_in_pauli_basis = PauliExpectation().convert(ng)
# 自然勾配を求める
def calculate_natural_gradient(params):
value_dict = dict(zip(qc_test.parameters, params))
result = sampler.convert(ng_in_pauli_basis, params=value_dict).eval()
return np.real(result)例として以下のような2量子ビットのパラメータ回路において、自然勾配を用いた最適化計算を確認しましょう。
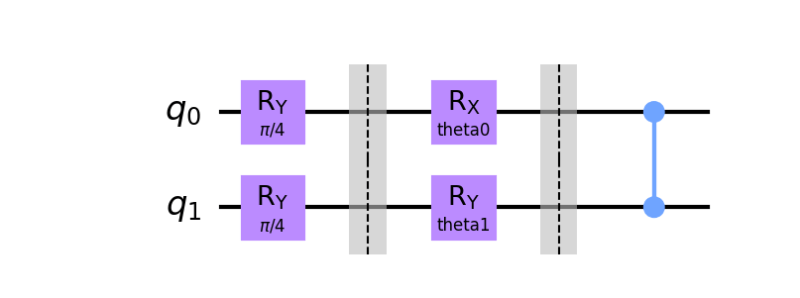
この量子回路はパラメータを持つ回転ゲートの層とパラメータを持たない制御Zゲートの層を1層ずつ持つ非常にシンプルな回路です。
なお、学習のためのコスト関数はシンプルにこの回路におけるXゲートの期待値としましょう。
# 期待値の計算
from qiskit import Aer
from qiskit.utils import QuantumInstance
from qiskit.opflow import CircuitSampler, StateFn, PauliSumOp
from qiskit.opflow.expectations import PauliExpectation
hamiltonian = PauliSumOp.from_list([('X', 1.0)])
expectation = StateFn(hamiltonian, is_measurement=True) @ StateFn(qc_test)
aerpauli_basis = PauliExpectation().convert(expectation)
quantum_instance = QuantumInstance(Aer.get_backend('qasm_simulator'),
shots = 32768)
sampler = CircuitSampler(quantum_instance)
# 期待値の評価
def calculate_exp_val(params):
value_dict = dict(zip(qc_test.parameters, params))
result = sampler.convert(aerpauli_basis, params=value_dict).eval()
return np.real(result)expectation = \langle\psi(\theta_0, \theta_1)|I\otimes X|\psi(\theta_0, \theta_1)\rangle
各パラメータ$(\theta_0, \theta_1)$毎のコスト関数の値を視覚化すると以下のようになります。
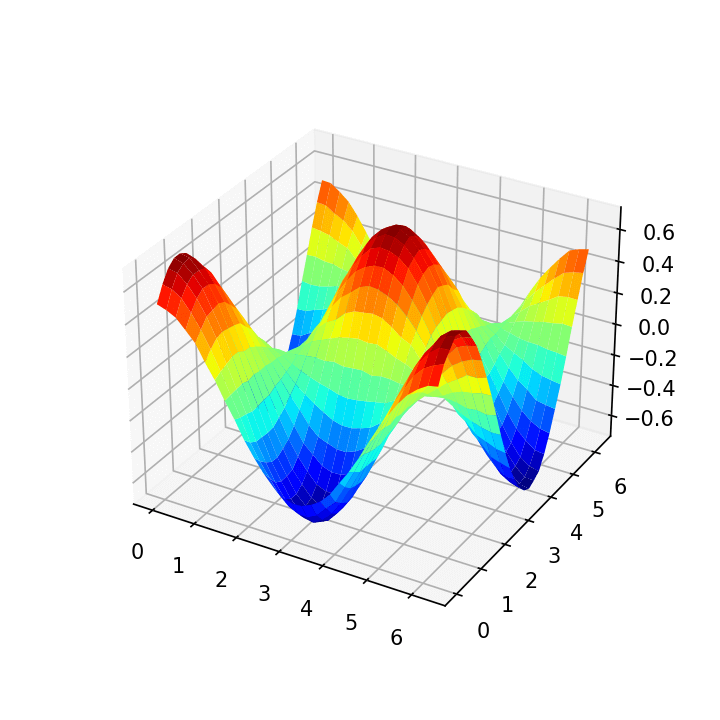
初期地点を選んで自然勾配降下により最適化を行います。
from qiskit.algorithms.optimizers import GradientDescent
initial_point = np.array([np.pi, np.pi])
ngd_loss= []
xx_op_ng= []
yy_op_ng= []
def ngd_callback(nfevs, x, fx, stepsize):
ngd_loss.append(fx)
xx_op_ng.append(x[0])
yy_op_ng.append(x[1])
qng = GradientDescent(maxiter=50,learning_rate=0.1, callback=ngd_callback)
x_opt_ng, fx_opt_ng, nfevs_ng = (
qng.optimize(initial_point.size,
calculate_exp_val,
gradient_function=calculate_natural_gradient,
initial_point=initial_point)
)結果は以下の通りです。収束の比較のため普通の最急降下法も併せて描画しています。
自然勾配を使った方がより速く収束していることが確認できました。
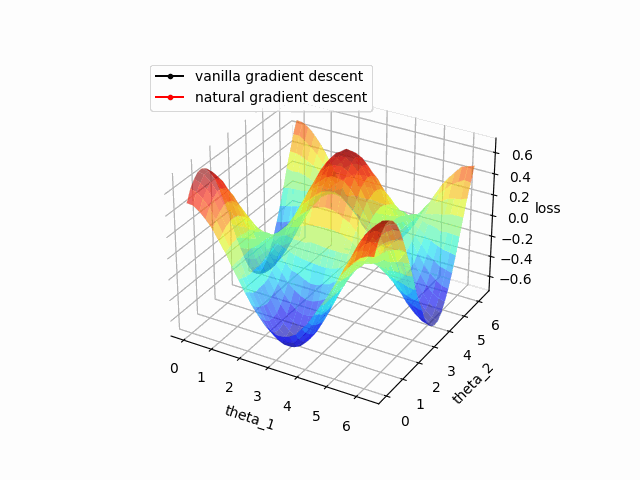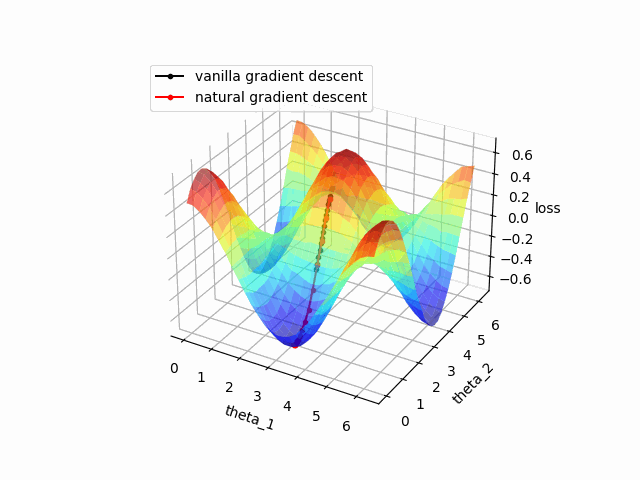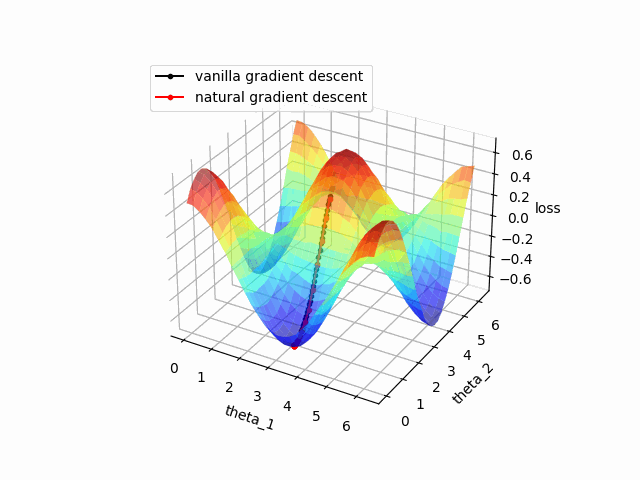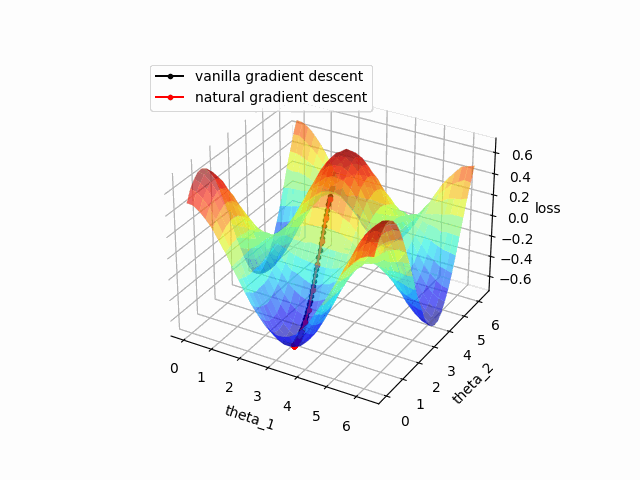
ただし、自然勾配は量子回路が大きくなるほど計算コストが大きくなるため実際には収束の速度と計算コストを比較しながら学習の設計を行う必要がある点には注意が必要です。
まとめ
この記事では自然勾配の特徴とQiskitの実装によるパフォーマンス評価のイメージを紹介し。
自然勾配はモデルの特性を取り込んだ概念で、招待は曲がった空間における最急降下法であることを確認しました。
また、Qiskitの実装を通して一例ではありますが最急降下法よりも高速に収束している様子も確認することが出来ました。








コメント