2020年3月に発表された初の量子コンピューティングの資格であるIBM QuantumのFundamentals of Quantum Computation Using Qiskit v0.2X Developer受験の手始めとして付属のサンプル問題の解説をしていきます。
試験概要はこちら、サンプル問題はこちらです。サンプル問題は全20問の4択形式となっています。
概要としては量子コンピューティングの概念的な知識や量子力学の学問的な理解を問うというよりは、PythonのオープンソースライブラリであるQiskitの利用に関する知識を問う試験となっているようです。
サンプル問題の解説
1. 量子回路の生成方法
4つの量子ビットと古典ビットを持つ量子回路の正しい生成方法を選択する問題です。
A. QuantumCircuit(4, 4)
B. QuantumCircuit(4)
C. QuantumCircuit(QuantumRegister(4, 'qr0'),
QuantumRegister(4, 'cr1'))
D. QuantumCircuit([4, 4])正解はAで、QuantumCircuitの引数に量子ビットの数と古典ビットの数を渡す必要があります。
Bは古典ビットが生成されず、量子ビットが4つだけの回路となります。
Cは引数にQuantumRegisterが渡されていることからもqr0というラベルの量子ビットとcr1というラベルの量子ビットを4つずつ持った量子回路が生成されます。
Dはコンパイルエラーとなります。
2. 観測時の状態の確率
与えられた量子回路から出力された状態を観測したときに0の状態の確率を問う問題です。
問題文のコードで与えられた量子回路を可視化します。
qc = QuantumCircuit(1,1)
qc.ry(3 * math.pi/4, 0)
qc.measure(0,0)
qc.draw('mpl')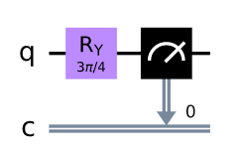
観測まで含めるため古典ビットを追加しています。単純に$\theta = 3\pi/4$のRyゲート(y軸回りの回転)を通した回路となっています。
結果を考えるにあたりまずはQiskit上で確認してみます。下の結果から0の状態が観測される確率は0.169であり、最も近いCが正解のようです。数値が正確に一致していないのはこのコードの書き方だと1024回観測した場合の確率分布を表しているためです(理論値は無限回)。
qasmsim = Aer.get_backend('qasm_simulator')
qobj = assemble(qc)
counts = qasmsim.run(qobj).result().get_counts()
plot_histogram(counts)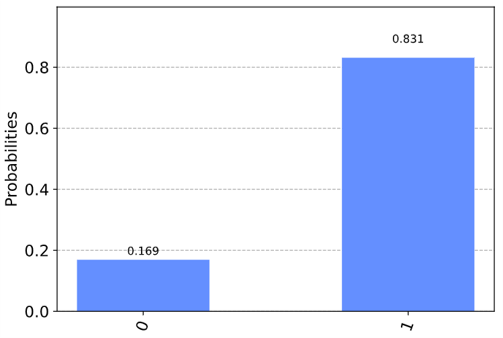
4択なので大雑把な値が求まれば答えは出せますが、正確な値をあえて計算で求めるとしたら一例として次のように考えることが出来ます。
Ryゲートをパウリゲートで分解すると次のように表せます。
$$R_y(\theta) = \cos \frac{\theta}{2}I – i\sin \frac{\theta}{2}Y$$
なので与えられた量子回路の出力は以下のようになります。
$$\begin{aligned}R_y(\theta)|0\rangle &= (\cos \frac{\theta}{2}I – i\sin \frac{\theta}{2}Y)|0\rangle \\ &= \cos \frac{\theta}{2}|0\rangle + \sin \frac{\theta}{2}Y|1\rangle\end{aligned}$$
よって$|0\rangle$が観測される確率は確率振幅の2乗を取ればよいので答えが求まります。$\theta = 3\pi /4$なので$\cos\theta = -1/\sqrt{2}$です。
$$|\cos \frac{\theta}{2}|^2 = \frac{1+\cos\theta}{2} \sim 0.1464$$
5. エンタングル状態となる量子回路
エンタングルメントが最大またはベル状態を出力する量子回路を選択する問題です。
エンタングルした状態(量子もつれとも言います)とは2つの量子状態が個別の量子状態のテンソル積で表せない状態を指します。特徴的なのがベル状態という量子状態です。ベル状態は数式では次のように表されます。
$$|B_00\rangle = \frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)$$
この2量子ビットの状態を個別の量子ビットの状態のテンソル積で表すことを考えます。つまり以下のように表現するということです。
$$|B_00\rangle = |\psi\rangle_A \bigotimes |\psi\rangle_B$$
ただし$|\psi\rangle_A = a_0|0\rangle+a_1|1\rangle, |\psi\rangle_B = b_0|0\rangle+b_1|1\rangle$です。
実はエンタングルした状態では上記を満たす量子状態が存在しない、つまり個別の量子ビットの状態のテンソル積で表せないのです。このように2つの量子状態が互いに相関し合った特別な状態であると言えます。
このような状態を一般的にどのように生成するのかという理論的な話は私も理解していないですが、素人感覚として、CNOTゲートを作用させる場合は出力がテンソル積で表せるとは限らない場合が多いです。
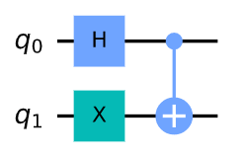
ちなみに解答はこちらの回路になります。
bell = QuantumCircuit(2)
bell.h(0)
bell.x(1)
bell.cx(0, 1)
bell.draw('mpl')こちらはベル状態を作る回路で覚えておいていいものではあつと思いますが、覚えてなくてもCNOTゲートを手掛かりにすれば2択に絞れるのでアウトプットを計算してみて確かめるという解き方もできそうです。
7. Sゲートの位相パラメータ
Z軸回りの回転ゲートであるRzゲートの中でも特に$\pi/2$回転と$\pi/4$回転を表すゲートにはそれぞれSゲート、Tゲートという特別な名前が与えられています。
従って解答はAの$\pi/2$です。
Sゲート、Tゲート、Zゲートの関係は次のようになります。回転角を考えれば自明ですね。
$$TT=S \\ SS=Z$$
8. 量子回路の穴埋め
与えられた状態ベクトルの出力となるような量子回路を作るように穴埋めをする問題です。与えられた2量子状態の状態ベクトルは数式に直すと次のように表せます。
$$\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)$$
これはベル状態なのでBは正しそうですね。
また、Aの書き方も状態ベクトルを指定して`.initialize()`で初期化するというqiskitのメソッドになり正解です。
qc = QuantumCircuit(2)
v = [1/math.sqrt(2), 0, 0, 1/math.sqrt(2)]
qc.initialize(v, [0,1])
simulator = Aer.get_backend('statevector_simulator')
result = execute(qc, simulator).result()
statevector = result.get_statevector()
print(statevector)
> [0.70710678+0.j 0. +0.j 0. +0.j 0.70710678+0.j]11. barrier()の使い方
barrierメソッドの使い方を問う問題です。問題文は全ての量子ビットにかかる区切りを入れる書き方を求めているので引数無しのCと全量子びぅとを指しているBが正解です。
# 正解
B. qc.barrier([0,1,2])
C. qc.barrier()
# 不正解
A. qc.barrier(qc)
D. qc.barrier(3)
E. qc.barrier_all()ここでDについては引数に指定されている量子ビットのインデックスが3であるため、3量子ビットの量子回路から溢れてしまいエラーとなってしまいます。ただし、もし引数を2とすれば最後の量子ビットのみに区切りを入れるという書き方になります。
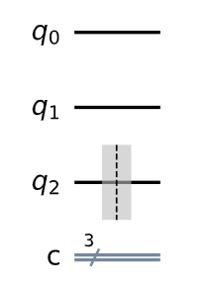
13. 量子回路の深さ
量子回路の深さとは入力から出力までに挟む量子ゲートの最大数を指します。
まずは問題で与えられているゲートを可視化します。
qc = QuantumCircuit(2, 2)
qc.h(0)
qc.barrier(0)
qc.cx(0,1)
qc.barrier([0,1])
qc.draw('mpl')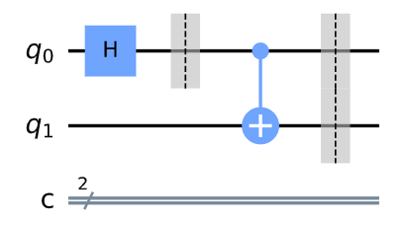
ここで$q_0$の状態が1の場合$q_1$のCNOTゲートは演算を行うためこの量子回路の深さは2と考えることが出来ます。実際にQiskitでは.depth()で求めることが出来ます。
print("Circuit depth: ", qc.depth())
> Circuit depth: 216. 利用可能なsimulator
BasicAerモジュール(Pythonベースの量子シミュレータ)で利用可能なシミュレータを選ぶ問題です。
https://qiskit.org/documentation/apidoc/providers_basicaer.htmlを参考にすると以下の3つが該当することがわかります。
- qasm_simulator
- statevector_simulator
- unitary_simulator
18. Xゲートと等価な演算子
Xゲートと等価な演算子を選択する問題です。
A. op = Operator.Xop(0)
B. op = Operator([[0,1]])
C. qc = QuantumCircuit(1)
qc.x(0)
op = Operator(qc)
D. op = Operator([[1,0,0,1]])答えは明らかにCですが、他の選択肢を確かめてみます。
AはXopという属性はOperaorオブジェクトには存在しません。
B,Dは表現行列から演算子を生成しようとしていますが、与えている行列がユニタリ行列でないためコンストラクター実行時にエラーとなります。
19. fidelity
fidelityの使い分けを問う問題です。グローバル位相のみが異なる2つの演算子間のfidelityとして正しい結果を選択します。
op_a = Operator(XGate())
op_b = numpy.exp(1j * 0.5) * Operator(XGate())ここで登場しているfidelityは3種類です。
state_fidelity()
state fidelityは2状態の類似度を表す指標で以下の定義で与えられます。ただし$\rho$は密度演算子です。
$$F(\rho_1, \rho_2) = Tr[\sqrt{\sqrt{\rho_1}\rho_2\sqrt{\rho_1}}]^2$$
状態が純粋状態の場合は$F = |\langle\psi_1|\psi_2\rangle|^2$
今回の問題では演算子間のfidelityを問うているのでこちらのfidelityは文脈に合わないと考えられます。
process_fidelity()
process fidelityは2つの量子チャネル(演算子)の類似度で与えられます。特に演算子がユニタリ演算子の場合はグローバル位相に拠らず、次のように定義されます。
$$F_{pro}(\Epsilon, U) = \frac{Tr[S_U S_{\Epsilon}]}{d^2}$$
$S$は各チャネルのスーパーオペレーターで、$d$は入力チャネルの次元です。Qiskitで実際に計算すると1と求まります。
op_a = Operator(XGate())
op_b = numpy.exp(1j * 0.5) * Operator(XGate())
process_fidelity(op_a, op_b)
> 1.0average_gate_fidelity()
average gate fidelityはprocess fidelityを用いて次のように表されます。
$$F_{ave}(\Epsilon, U) = \frac{dF_{pro}(\Epsilon, U)+1}{d+1}$$
従ってprocess fidelityが1ならaverage gate fidelityも1です。
op_a = Operator(XGate())
op_b = numpy.exp(1j * 0.5) * Operator(XGate())
average_gate_fidelity(op_a, op_b)
> 1.0まとめ
問題を通してQiskitの基本的な記述方法を問う問題も多く含まれていることがわかります。受験の際はあいまいな部分を潰してから試験に臨んだ方がよさそうですね。








コメント