量子回路学習(Quantum Circuit Learning: 以下QCL)とは、NISQ(Noisy Intermediate-Scale Quantum Computer)デバイスにおいて機械学習を行うための量子アルゴリズムです。
QCLは有名な量子アルゴリズムであるVQEの「試行関数を変分的に最適化する」という概念を機械学習のタスクに拡張した概念です。VQEではエネルギー期待値を最小化するようにパラメータを最適化しますが、量子回路学習では損失関数を最小化するようにパラメータを最適化します。
はじめに
本記事はこちらの元論文を元に執筆しています。
- 機械学習のプロセスの理解
- VQEアルゴリズムの概念の理解(あればなお良い)
QCLアルゴリズムの流れ
QCLのアルゴリズムは以下のとおりです。
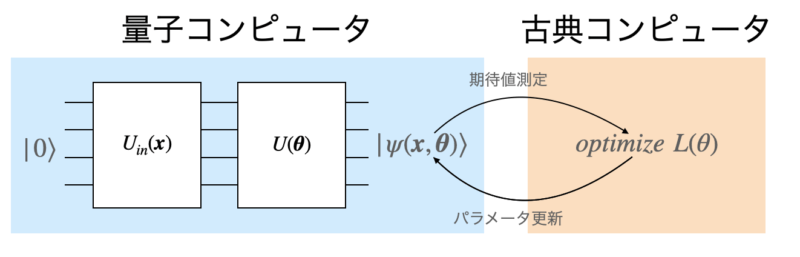
- 教師データの入力${x_i}$をパラメータとする量子回路$U_{in}(\bm{x})$を作用させて、データ${x_i}$をエンコードした量子状態$|\psi_{in}(\bm{x})\rangle$を作る。
- 入力状態$|\psi_{in}(\bm{x})\rangle$に対してパラメータ化量子回路$U(\theta)$を作用させて状態$|\psi_{out}(\bm{x, \theta})\rangle = U(\theta)|\psi_{in}(\bm{x})\rangle$に変換する。
- 量子ビットを適当なオブザーバブルで測定する。
- 得られた値と教師データ${y_i}$の差分を評価する損失関数$L(\theta)$を計算し、差分が最小になるようなパラメータ$\theta^*$を求める。
$\theta^*$でパラメータ化されたモデル(量子回路)は出力と教師データの差分が最も小さくなるように構築されるため、このモデルを使って未知の入力に対する予測値を求めることができます。
QCLアルゴリズムの特徴
QCLが古典コンピューター上のニューラルネットワークなどの機会学習と比較したときの特徴は主に2点です。
- 量子ビット数に対して指数関数的に多くの基底関数を利用することができる
- ユニタリ変換のみで構築されたモデルは過学習が抑えられる可能性がある
これらの特徴については以下で説明します。
指数関数的に多くの基底関数を利用することができる
例として$x$がスカラーの場合を考えましょう。入力ゲート$U_{in}$には単純な回転ゲート
$$U_{in}(x)|0\rangle = x|0\rangle + \sqrt{1-x^2}|1\rangle$$
を考えます($x$を変化させることで任意の回転を表現できます)。このゲートをnqubitそれぞれに作用させると、得られる量子状態は以下のようになります。
$$|\psi (x)\rangle = (x|0\rangle + \sqrt{1-x^2}|1\rangle)^{\bigotimes n}$$
テンソル積の構造から、適切なオブザーバブルでこの状態を測定すれば例えば$\sqrt{1-x^2}$や$1-x^2$など元のデータ$x$に対する非線形項が現れます。
このように単純な1量子ビットの回転ゲートを用いても、複数量子ビットのテンソル積構造によってデータ$\bm{x}$を非線形関数で変換して振幅エンコーディングすることができます。この非線形項は量子ビットの数に対して指数関数的に増やすことができるためモデルの表現力を高めることができると考えられています。
モデルの過学習を抑えられる可能性がある
量子回路の特徴としてすべてモデルの構築はユニタリ変換を通して行われているため、線形回帰では重みパラメータである$\bm{\theta}$はノルムが常に1である必要があります。
この制約条件がある種の正則化として働き、古典モデルと比較して過学習を起こしにくいと言われています。
正則化とはモデルが過学習を起こさないための工夫のことで、馴染みのない方はこちらをご覧ください。
QCLを実装する
こちらの記事でQiskitを使って実際にQCLの量子回路を組んで$y = \sin x$の回帰問題を解いてみましたので実装まで興味のある方はこちらをご覧ください。









コメント