量子コンピュータの応用先の一つとして物理系のシミュレーションが挙げられます。
物理系のシミュレーションはあらゆる場面で使われていて、最近の話題だと電車内のウイルスの散布状況の時間変化の解析などが挙げられます。シミュレーションの目的は、それぞれ何らかの基礎方程式に従う物理系がどのように時間発展するかを知ることです。
現状のシミュレーションにはほぼすべての場面で古典コンピュータが使われていますが、指数関数的に計算コストが増えてしまう量子系のシミュレーションはすぐに限界を迎えると言われています。
そこで量子コンピュータを用いて量子系のシミュレーションも可能にしようというのが背景です。
はじめに
本記事はQuantum Native Dojo 4章「量子ダイナミクスシミュレーション」を元に執筆しています。
量子系のシミュレーション
基礎方程式とは高校物理で習った運動方程式や電磁気学系のMaxwell方程式など物理系の振る舞いを決定づける方程式のことを指します。量子系ではシュレーディンガー方程式と呼ばれる方程式に従った振る舞いをします。
$$i\hbar\frac{\partial}{\partial t}\psi = \hat{H}\psi$$
系が時間依存しないときの状態変化はシュレーディンガー方程式を解いて以下のように表すことができます。
$$\psi(t) = e^{-i\frac{\bar{H}}{\hbar}t}\psi(0)$$
Quantum Native Dojoではハミルトニアンとして横磁場イジングモデルを扱っています。イジングモデルとは物理の文脈でよく使われる磁性体(磁石)をモデル化したものです。
$$\hat{H} = \sum_{i=1}^nZ_iZ_{i+1} + h\sum_{i=1}^nX_i$$
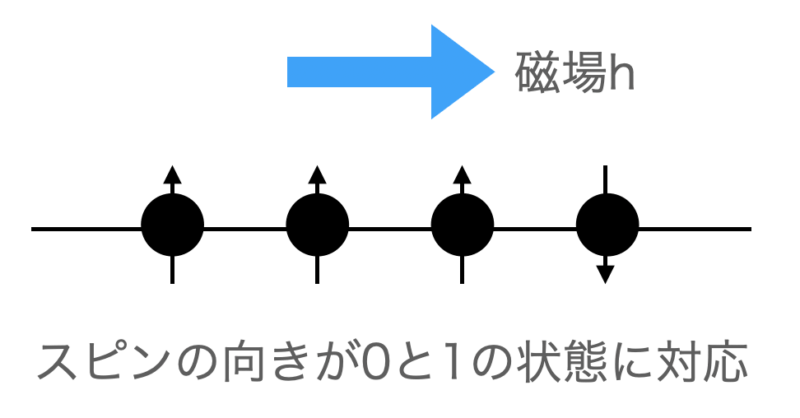
今回は磁化(どれだけ状態が揃っているか)の時間変化を追跡することをゴールとしています。そのため各量子ビットのZ成分を測定すれば磁化を得ることができます。つまり、期待値は下の数式で表すことができます。
$$M(t) = \left\langle\psi(t)\right|\sum_i Z_i\left|\psi(t)\right\rangle$$
つまり私達がシミュレーションするにあたって必要なことは以下の2つです。
- $\psi(t) = e^{-i\frac{\hat{H}}{\hbar}t}\psi(0)$に従って状態変化をする量子回路を用意する
- 任意の時刻で各量子ビットのZ方向を測定して期待値を求める
1の量子回路の部分についての詳細はQuantum Native Dojoをご覧ください。
Qiskitの実装
以上を念頭にQiskitを用いて実装していきます。
ライブラリのインポート
まずは必要なライブラリをインポートします。
from qiskit import *
from qiskit import Aer
from qiskit.aqua import QuantumInstance
from qiskit.aqua.operators import Z
from qiskit.aqua.operators.state_fns import StateFn, CircuitStateFn
from qiskit.aqua.operators.expectations import PauliExpectation, AerPauliExpectation
from qiskit.aqua.operators.converters import CircuitSampler
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import matplotlib.colors as colors
import numpy as np
%matplotlib inline定数の定義
続いて必要な定数を定義します。今回は6ビット使用してシミュレーションします。
nqubits = 6 # 量子ビット数
sv = 2**nqubits # 状態数
t = 3.0 # ダイナミクスをシミュレーションする時間
M = 100 # トロッター分解の分割数
delta = t/M # 時間の刻み幅
h = 3 # 外部磁場期待値を求める関数を実装
今回のシミュレーションでは磁化の期待値をシミュレーションしたいので、期待値を求める関数を実装します。引数のpsiは状態ベクトル、opは演算子を表しています。
def get_expectation_val(psi, op):
backend = Aer.get_backend('qasm_simulator')
q_instance = QuantumInstance(backend, shots=1024)
measurable_expression = StateFn(op, is_measurement=True).compose(psi)
# expectation = PauliExpectation().convert(measurable_expression)
expectation = AerPauliExpectation().convert(measurable_expression)
sampler = CircuitSampler(q_instance).convert(expectation)
return sampler.eval().real量子回路の実装
それではメインの量子回路部分を実装します。
#回路の準備
circuit_trotter_transIsing = QuantumCircuit(nqubits)
# 初期状態の準備
print("{}ビットの初期状態を入力してください。重ね合わせは'+'。(例:000+)".format(nqubits))
b_str = input() # 入力ビットのバイナリ列
for qubit in range(len(b_str)):
if b_str[qubit] == '1':
circuit_trotter_transIsing.x(qubit)
elif b_str[qubit] == '+':
circuit_trotter_transIsing.h(qubit)
arr = [] #結果を格納する配列
# 計算
for s in range(M):
# トロッター分解の1回分、
for i in range(nqubits):
circuit_trotter_transIsing.cx(i,(i+1)%nqubits)
circuit_trotter_transIsing.rz(-2*delta,(i+1)%nqubits)
circuit_trotter_transIsing.cx(i,(i+1)%nqubits)
circuit_trotter_transIsing.rx(-2*delta*h, i)
# 磁化の期待値を求める
psi = CircuitStateFn(circuit_trotter_transIsing)
op = Z
result = get_expectation_val(psi, op)
#状態ベクトルの保存
arr.append(result)Trotter分解によりM分割して1回分($\delta=t/M$の時間発展)の回路を実装し、磁化を測定するという処理を行います。
シミュレーション結果
# 磁化ダイナミクス表示
x = [i*delta for i in range(M)]
plt.xlabel("time")
plt.ylabel("magnetization")
plt.plot(x, arr)
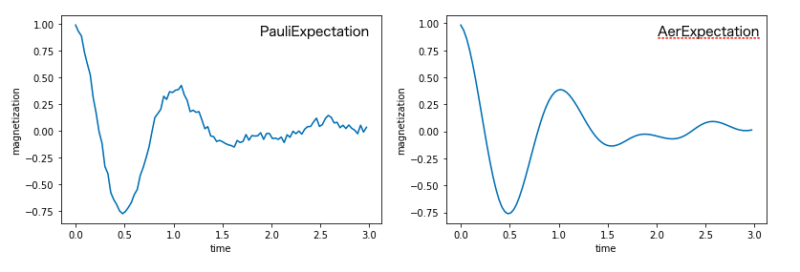
plt.show()下がシミュレーションの結果です。左右の違いは測定方法です(get_expectation_valのコメント部分)。左は1024回分の測定から期待値を計算しているため厳密な数値計算の理想的な結果よりもノイズが大きくなっています。このように正しく実装ができました。
実機を用いる場合の注意
今回のシミュレーションでは
Trotter分解した1回分の量子回路を構築→磁化測定→次の1回分の量子回路を構築→磁化測定→
という処理ループとなっていますが、この処理は実際には問題があります。
一般に量子状態を測定すると状態が確定するため重ね合わせが壊れて状態が変化してしまいます。そのため測定後の状態は測定前の状態と異なるため上記の処理では本来は正しいシミュレーションができません。今回はシミュレーションということで計算時間を短縮するために上の処理にしています。
実機でシミュレーションする場合は各時間に対応する量子回路を準備して別々に演算と測定をする必要があるという点は注意が必要です。








コメント